Big Data, Big Trouble: Selectiebias

Deze post is origineel verschenen op Mark’s eigen blog.

Nullen en Enen

Om de blits te maken bij een eerstejaars college kansrekening voert een docent (m/v) het volgende experiment uit¹. Ongezien vraagt hij tien studenten een willekeurig rijtje van 200 nullen en enen in te voeren, en ook de computer 10 zulke rijtjes te laten genereren. Dan komt de magie: de docent pikt behoorlijk nauwkeurig de studenten rijtjes eruit. Hoe doet ie dat? Hij schrijft van elk rijtje de maximale run (= opeenvolging van identieke getallen) op, en kiest simpelweg de tien rijtjes met de kortste maximale run. Waarom werkt dit? Wanneer wij mensen zo’n rijtje nullen en enen opschrijven, zien we op een gegeven moment vijf nullen achter elkaar. Die gebeurtenis isoleren we, en we nemen een besluit op basis daarvan. Vijf nullen achter elkaar is toch wel erg onwaarschijnlijk: laat ik maar weer eens een één opschrijven. Zowel de selectie (de vijf nullen), als de bias (het volgende getal is niet willekeurig gekozen) zijn in dit ‘kleine Big Data’ voorbeeld subtiel en vrijwel onbewust aanwezig.

20,000 correlaties

Een voorbeeld uit mijn eigen praktijk. Stel we correleren 20,000 genen met ziektebeloop op basis van data van 50 mensen. We berekenen 20,000 correlatiecoëfficiënten (0: ongecorreleerd; -1 resp. 1 : maximaal negatief resp. positief gecorreleerd). We willen natuurlijk weten welke correlaties significant zijn. Gelukkig weten we inmiddels dat we netjes moeten corrigeren voor ‘multiple testing’. Hoera, vier genen zijn significant, en wauw, stevige correlaties: -0.7, -0.5, 0.6, 0.8. Menig wetenschappelijk artikel meldt dan: vier significante genen met deze vier correlaties. Maar helaas: hier is sprake van bewuste selectie met onbewuste bias. Als men een paar maanden later de resultaten wil valideren door deze vier genen te meten op een nieuwe groep mensen, dan vindt men slechts -0.2, -0.1, 0.1 en 0.3. Een veel minder sterk verband, en dus ook veel minder relevant. In sporttermen: de vier genen versloegen 19,996 concurrenten in de eerste wedstrijd, en leverden dus een ongelooflijke prestatie (= de vier grote correlaties). De kans dat ze die prestatie kunnen herhalen is klein: de vloek van de winnaar(s).

Oude wijn in nieuwe zakken

Wat is hier aan de hand? Selectiebias: als je extremen selecteert, zullen de effecten hiervan vaak kleiner worden bij validatie. Voor veel statistici een bekende gruwel, voor medische vakbladen een onderkend fenomeen. Ik zie zo veel artikelen waarin de effectgroottes schromelijk zijn overschat door selectiebias. Overigens: niks nieuws onder de zon. Het is gerelateerd aan Frances Galton’s ‘regressie naar het gemiddelde’ fenomeen² (zie Figuur 2). Zoals je verwacht dat in het genetisch voorbeeld de effecten bij het origineel experiment lijken op die van de validatie, zo verwacht je ook een relatie tussen de lengte van ouders en hun kinderen. Galton legde in 1886 met dit figuur uit dat dit inderdaad zo is. Maar ook dat er een verwatering optreedt: de minder steile, doorgetrokken lijn verklaart de data beter dan de diagonale, gestreepte lijn. Bij lange of korte ouders (de extremen dus) zullen de lengtes van de kinderen dichter bij het algemeen gemiddelde liggen. En zo zullen de validatie correlaties van de geselecteerde genen ook veel dichter bij het algemeen gemiddelde (vaak ongeveer nul) liggen dan de originele correlaties.

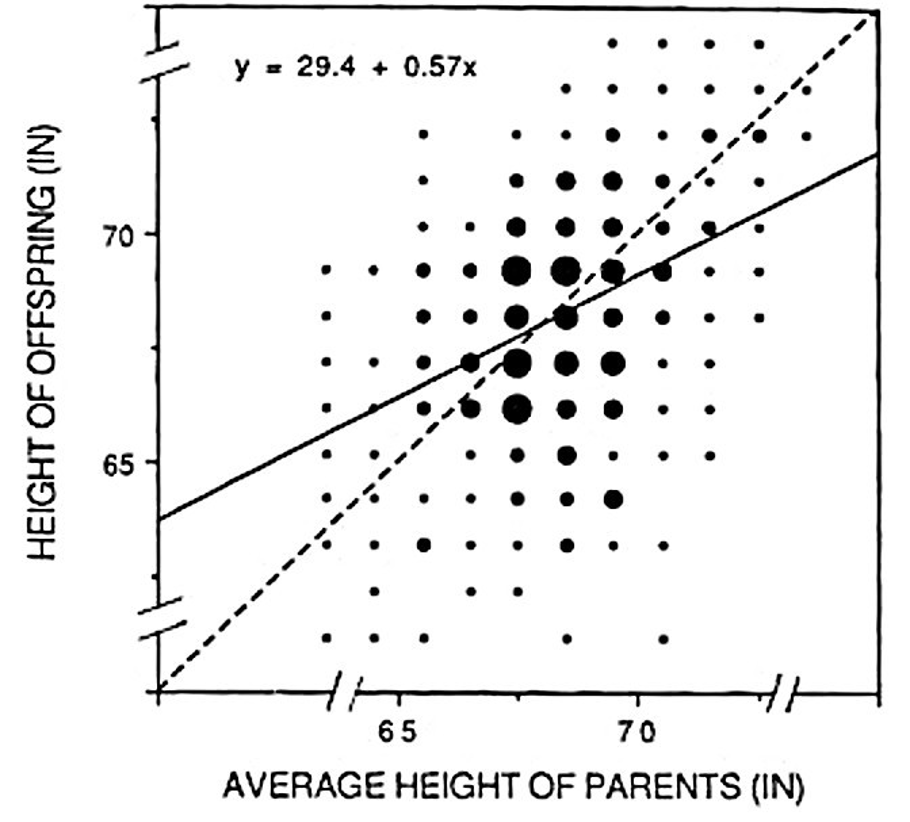
Het reeds lang bekende regressie naar het gemiddelde fenomeen en selectiebias zijn dus zusjes. De ellende van Big Data is dat de bias veel groter is als je uit veel selecteert. Hadden we bovenstaande vier genen uit 20 genen (ipv 20,000) genen geselecteerd, dan hadden we bij de validatie wellicht -0.6, -0.4, 0.5, 0.7 gevonden: veel dichter bij de originele waardes. Hier zit de crux van het probleem: we weten vaak niet hoe groot de bias is, en hoe deze zich verhoudt tot het aantal waaruit we hebben geselecteerd.

Foute tip

U kunt er uw voordeel mee doen als u zich bewust bent van de selectie én de bias. Stel, u wilt een duur nep-middel tegen hoge bloeddruk verkopen. Moet u toch iets van bewijs voor hebben. Meet de bloeddruk bij 10,000 mensen. Selecteer dan de 100 mensen met de hoogste bloeddruk (“het is immers een middel tegen hoge bloeddruk”). Geef die mensen twee weken het middel: ik garandeer u dat na twee weken de gemiddelde bloeddruk in deze groep gedaald is. Ik zie de slogan al voor me: “Wetenschappelijk aangetoond: revolutionair middel verlaagt de bloeddruk”. Moraal van het verhaal: selectiebias wordt misbruik als je er niet bij zegt dat je hebt geselecteerd.

Oplossingen

Het begint dus bij onderkennen van het probleem. Vermeld altijd de dimensie: het aantal items waaruit geselecteerd is. Hoe hoger de dimensie, hoe groter het selectiebias probleem. Om de selectiebias te bestrijden zijn er krimpschatters. Krimpen (Eng: shrinkage) is een geavanceerde statistische techniek om bij hoge dimensie een betere schatting van de effectgroottes te geven. Uw statisticus kan u hiermee helpen, want dit moet behoren tot de gereedschapskist van de moderne statisticus. Een mooie oplossing die helpt de verwachtingen qua effecten te temperen, maar zeker niet vrij van aannames. De enige echte oplossing heb ik al genoemd: validatie, mits goed uitgevoerd – altijd op een nieuwe groep mensen – én tegelijkertijd gepresenteerd met de originele data. Ook heel leerzaam om zo een volgende keer beter te kunnen inschatten hoe duivels groot het selectiebias probleem kan zijn.

Referenties

¹Schilling, M. F. (1990). The longest run of heads. The College Mathematics Journal, 21(3), 196-207.
²Galton, F. (1886) Regression towards mediocrity in hereditary stature. Journal of the Anthropological Institute of Great Britain and Ireland, 15, 246– 263.