Geen effect gevonden, bestaat het dan ook niet?

Deze post is origineel verschenen op Carolien’s LinkedIn pagina.

Hoe toon je effect aan?

Een effect van bijvoorbeeld een medicijn onderzoek je door twee groepen patiënten te nemen, de ene groep krijgt het medicijn, de andere niet. Na verloop van tijd worden die twee groepen vergeleken. Elke vergelijking van twee groepen begint met het opstellen van twee hypothesen: de nulhypothese die stelt dat er geen verschil is, en de alternatieve hypothese die stelt dat er wel een verschil is. Omdat wetenschappers niet graag foutief melden dat er een verschil is, dus dat er een effect is van het medicijn, geven ze de nulhypothese heel lang het voordeel van de twijfel. Eigenlijk net zo als in de rechtspraak: de verdachte (nulhypothese) krijgt het voordeel van de twijfel dat hij niet schuldig is (niet verworpen moet worden), tot het alternatief wettig en overtuigend bewezen is. In het geval van statistische hypotheses betekent dat, dat pas als het verschil tussen de groepen erg groot is, ze zeggen dat een effect wel is aangetoond. Hoe groot dat verschil moet zijn, hangt af van hoe groot de groepen zijn die worden bestudeerd, dus in het voorbeeld, hoeveel patiënten er wel en niet het medicijn krijgen.

Een verschil in proporties aantonen valt niet mee

Stel nu dat we veertig patiënten het medicijn geven en veertig patiënten niet. Na een bepaalde periode zien we dat van de patiënten met medicijn 53% extra zuurstof nodig heeft en zonder medicijn 73%. Een fors verschil: 20 procentpunten. Dit lijkt een groot verschil, maar dit is niet significant: het kan dus best toeval zijn dat de studie zo uitpakt. Maar als je echt 20 procentpunt verschil zou hebben tussen medicijn en geen medicijn, is de kans dat je dat met groepsgroottes van twee keer veertig patiënten statistisch kunt aantonen erg klein. Je zou dan al gauw negentig patiënten in elke groep moeten hebben. Dan is een verschil van 53% vs 73% door toeval niet meer waarschijnlijk en noemt men dat verschil significant.

Zou het verschil in werkelijkheid kleiner zijn, bijvoorbeeld 53% vs 63%, dan heb je al snel een paar honderd patiënten nodig in elke groep om een verschil te kunnen aantonen. Dus als de groepen relatief klein zijn, dan moet je een uitspraak als ‘geen significant verschil’ zeker niet zonder meer interpreteren als ‘er is geen verschil’. Je kunt het gewoon niet weten. Zijn de groepen wel heel groot en is de conclusie van de onderzoekers ‘geen significant verschil’ dan kun je er al redelijk vanuit gaan dat er waarschijnlijk geen groot verschil is.

Belangrijk: geen significant verschil kan betekenen dat er in de werkelijkheid inderdaad zo goed als geen verschil in proporties is tussen de groepen, maar ook dat het verschil te klein is om aan te tonen. Om verschillen in proporties aan te kunnen tonen, kunnen behoorlijk grote steekproeven nodig zijn.

Een verschil in meetwaardes aantonen hangt af van de overlap

In plaats van proporties kun je ook meetwaarden willen vergelijken. Je vergelijkt bijvoorbeeld het gemiddeld aantal dagen dat patiënten in het ziekenhuis liggen met en zonder het medicijn. En dan geldt hetzelfde: geen verschil aangetoond betekent niet per se dat er geen verschil bestaat. Ook hier geldt dat je om een klein verschil aan te tonen grote groepen moet vergelijken. De patiënten in de twee groepen liggen niet allemaal hetzelfde aantal dagen in het ziekenhuis. Ook binnen de groepen bestaat variatie.

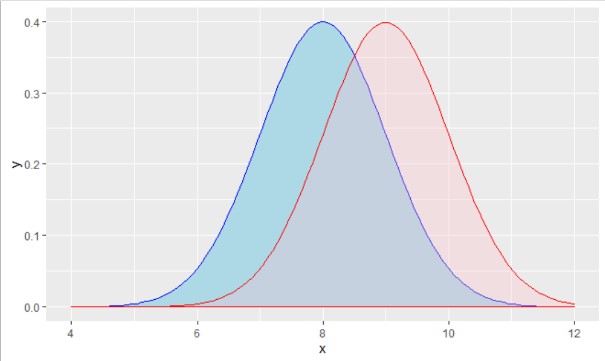
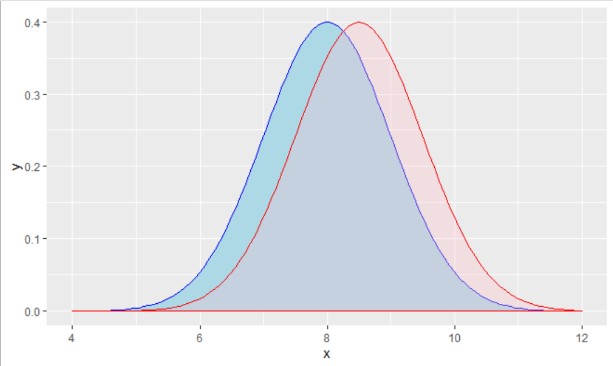
Kijk even naar het linker plaatje dat de verdeling laat zien van het aantal ziekenhuisdagen in de groep met (blauw) en de groep zonder (roze) medicijn. De overlap in het aantal ziekenhuisdagen tussen beide groepen is links ongeveer 60%. Als je groepen hebt van zo’n 25 patiënten elk, dan was een verschil zo groot als in de linker figuur waarschijnlijk wel aangetoond. Een verschil zo groot (klein) als rechts (overlap 80%) had men kunnen missen. Daarvoor heb je al zo’n zeventig patiënten per groep nodig.

Het verschil dat is aan te tonen hangt niet zo zeer samen met hoeveel dat in absoluut aantal dagen is, maar met hoeveel overlap er is tussen de verdelingen van de twee groepen.

Belangrijk: Ook bij meetwaardes bepaalt de grootte van de groepen hoe groot het verschil is dat je waarschijnlijk wel of waarschijnlijk niet kunt aantonen. Dus ook in dit geval moet een ‘niet significant verschil’ worden geïnterpreteerd als mogelijk zo goed als geen verschil, maar mogelijk ook een verschil dat kleiner is dan een waarde die samenhangt met de aantallen patiënten in de studie.

Om geen foute conclusies te trekken, geven statistici de nulhypothese, dus de hypothese van ‘geen verschil’, het voordeel van de twijfel. Bedenk altijd dat bij die twijfel de grootte van de groepen in de studie een rol speelt: kleinere groepen, meer twijfel.