“Patiënten met aandoening X slapen significant korter dan gezonde mensen.” Ja, leuk om te weten, maar de volgende vraag is natuurlijk: hoeveel korter? Is het gemiddeld tien minuten of gemiddeld anderhalf uur. Dat maakt natuurlijk uit. Of “Scores op CITO-toetsen hangen significant samen met het inkomen van de ouders”. Dan wil je toch weten hoe belangrijk dat inkomen is voor de CITO-scores van kinderen. Is het de belangrijkste factor of zijn er andere dingen die een veel grotere invloed hebben? Statistici hebben verschillende manieren om uit te drukken hoe groot effecten zijn. Om beter te begrijpen of een significant effect ook relevant is voor jou als lezer van een artikel of rapport, is een beetje idee van deze effectmaten best handig.
Weet wat je meet
Als het verschil in de gemiddelde uren slaap tussen de zieke en de gezonde deelnemers aan een studie anderhalf uur is, dan kunnen we dat gemakkelijk interpreteren. Als ik elke nacht anderhalf uur minder slaap, merk ik dat echt wel. Om een effectgrootte te kunnen interpreteren, moeten we ons er iets bij kunnen voorstellen. Anderhalf uur op een nacht slaap is veel, op een mensenleven verwaarloosbaar.
Een kleine zijsprong. Een onderzoek wordt normaalgesproken niet gedaan aan alle gezonde en alle zieke mensen, maar aan een representatieve selectie van mensen. Om het behapbaar te houden. Het gemiddelde in zo’n selectie (steekproef) kan door toeval net wat afwijken van de totale groep. In een net rapport zie je daarom ook nog een betrouwbaarheidsinterval. Je ziet dan iets als ‘Het verschil is anderhalf uur (95% CI 1,0-2,0). Zonder op details in te gaan, betekent dit dat als we alle mensen hadden gemeten, het verschil hoogstwaarschijnlijk een getal ergens tussen een en twee uur was geweest. Nou ja, een gemiddeld verschil van één uur per nacht is natuurlijk nog steeds aanzienlijk, en twee uur zeker.
Als je niet echt weet wat je meet
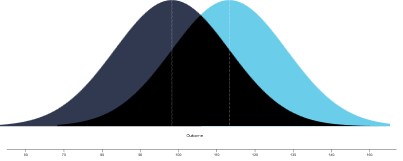
Als wat we meten niet zo gemakkelijk te interpreteren is, doen we het anders. Stel je vraagt mensen op een schaal van 1 tot 10 aan te geven hoe lekker ze een nieuwe variant pindakaas vinden. En het blijkt dat kinderen hem gemiddeld anderhalve punt minder lekker vinden dan volwassenen. Wat zegt dat? In dat geval hebben statistici een hele reeks maten in de kast om dat uit te drukken. Een veelgebruikte maat is Cohen’s d (naar de Amerikaanse onderzoeker Jacob Cohen). Die maat laat zien hoe veel overlap er is tussen de twee groepen. Een waarde van één betekent dat het verschil tussen de twee gemiddeldes even groot is als de standaarddeviatie. Hieronder zie je twee verdelingen die een verschil hebben van d=1. Op webpagina https://rpsychologist.com/cohend/ kun je spelen met andere d-waarden. Is d=1 een groot of een klein effect? Veel onderzoekers vinden dit best een groot effect, omdat de overlap van de twee verdelingen nog geen 70 procent is. En onderzoekers vinden meestal een verschil belangrijker naarmate er minder overlap is tussen twee groepen. Klinkt niet onredelijk, toch? Maar ook hier zul je als lezer uiteindelijk zelf moeten bedenken of het voor jou relevant is.
R2 : verklaarde variantie
Een verschil tussen twee gemiddelden is nog redelijk goed voor te stellen, maar we hebben ook vaak te maken met een relatie tussen twee (of meer) dingen die aan een persoon of een voorwerp gemeten zijn. Bijvoorbeeld de relatie tussen het ouderlijk inkomen van iemand en diens schoolprestaties of het alcoholpercentage in iemands bloed en diens reactiesnelheid. Als die relatie significant is, wil je toch weten: ja, maar hoe belangrijk is bijvoorbeeld dat alcoholpercentage nu? Zijn de natuurlijke verschillen tussen mensen niet veel belangrijker dan het effect van alcohol? De sterkte van zo’n verband wordt vaak uitgedrukt in een R2-waarde. De betekenis van die waarde is ‘de proportie variatie in de uitkomsten (schoolprestatie of reactiesnelheid) die verklaard kan worden door de variatie in de andere maat (ouderlijk inkomen of alcoholpercentage)’. Is de R2-waarde nul, dan heeft bijvoorbeeld ouderlijk inkomen totaal geen relatie met de schoolprestaties. Of kinderen rijke, arme of modaal verdienende ouders hebben, maakt dan voor hun schoolprestaties niets uit. Is de R2-waarde gelijk aan één, dan is het ouderlijk inkomen voor honderd procent ‘verantwoordelijk’ voor de verschillen. Geen andere factoren zijn dan van belang om schoolprestaties te begrijpen: geen gezondheid, geen gender, zelfs geen belemmeringen als dyslexie of ADHD.
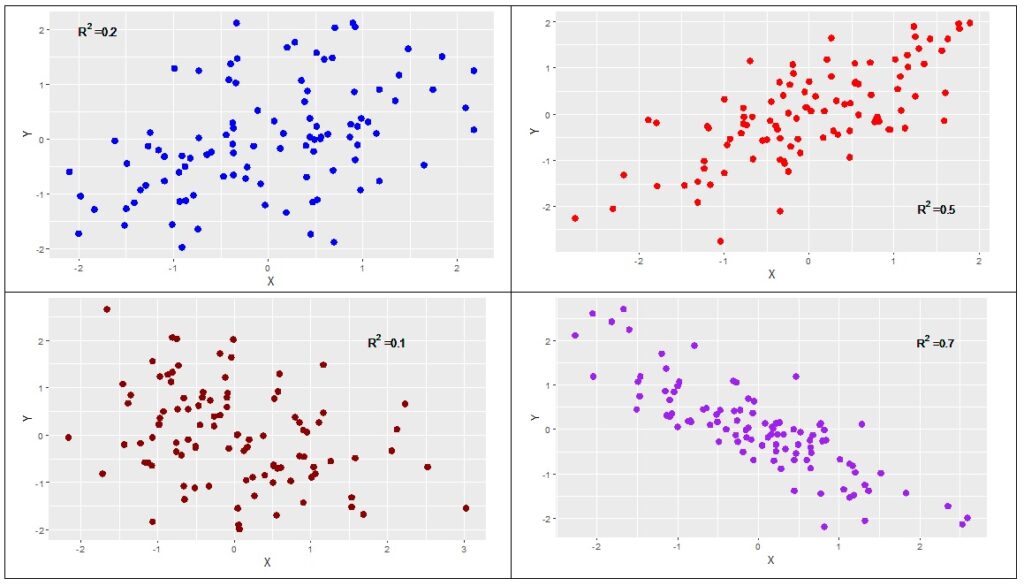
Natuurlijk zul je meestal R2-waardes tussen nul en één zien. En ik ga niet zeggen of R2=0,1 relevant is of pas R2=0,7. Dat hangt toch echt af van waar we het over hebben. Opnieuw is het belangrijk te weten wat er precies is gemeten. Als er een grafiekje is, kijk daar dan ook naar. In de figuur hieronder zie je een aantal R2-waarden gevisualiseerd. Stel dat linksboven de relatie tussen ouderlijk inkomen en CITO-scores weergeeft, vind je dat dan erg? Of pas als het om het plaatje rechtsboven gaat?
Een betrouwbaarheidsinterval voor R2 wordt vaak niet gegeven, maar je kunt ook hier ervan uitgaan dat wanneer onderzoekers alle mensen hadden gemeten in plaats van een steekproef, de uitkomst van R2 net ietsje anders zou zijn geweest.
Moet je boos worden?
Als onderzoekers grote steekproeven hebben, dus als ze veel data hebben verzameld, dan kunnen ze heel gedetailleerd kijken. Een verschil in gemiddelde nachtrust van 10 minuten kunnen ze dan bijvoorbeeld al opmerken. Met kleine steekproeven zien ze zo’n verschil gemakkelijk over het hoofd.
Hoe dan ook, als je leest dat er significante resultaten zijn gevonden in iets wat je interessant vindt, lees dan even verder om uit te vinden hoe groot de ‘effecten’ zijn. En kijk naar grafieken als die er zijn. Is het effect groot genoeg om je zorgen te maken, boos te worden of in actie te komen of valt het mee?
Referenties
Op deze webpagina kun je Cohen’s d variëren om te zien wat voor overlap dat geeft: https://rpsychologist.com/cohend/ [ENG]
Op deze webpagina kun je variëren met correlaties om te zien hoe verschillende verbanden eruit zien. https://shiny.rit.albany.edu/stat/rectangles/ [ENG]













Beste Carolien,
Ik ben ook VVSOR lid en bezig geweest met de archiefdigitalisering. Maar ik heb helaas ook een hersenletsel, oa schade in de Pars Triangularis. Over die PT vond ik een artikel:
https://psychology.fandom.com/wiki/Triangular_part_of_inferior_frontal_gyrus#cite_note-14
die een verbans met Schizofrenie suggereert maar dat wordt totaal ontkend bij UMC Psychiatrie. Na een eerder onderzoek bij Vesalius en Riagg werd wel DSM diagnose schizotypie vastgesteld. Ik heb volgens mij ook wel wat schizo trekjes.
De totale ontkenning van de relevantie voor mij van voornoemd artikel zit me nog niet lekker. Het verhaal bij UMC was dat de spreidingen in de populaties met en zonder PT schade te groot zou zijn om er voor een individu een conclusie uit te trekken. Lijkt me stug maar ondanks mijn eigen exacte achtergrond kan ik de UMCer niet overtuigen van zijn gedeeltelijk ongelijk.
Kun jij hier iets aan toevoegen?
Met vriendelijke groet,
Harm Schut