Onzekerheid hoort bij onderzoek

Deze blogpost verscheen eerder op Wetenschap.nu.

Onderzoekers proberen de onnauwkeurigheid van hun resultaat te laten zien door de kans aan te geven met een interval. Bijvoorbeeld een kans van 10 tot 14 procent. Om dit uit te leggen, moeten we eerst wat weten over puntschatters en betrouwbaarheidsintervallen. Laten we hiervoor kijken naar een simpel voorbeeld.

De gemiddelde lengte van de Nederlandse vrouw

Stel dat we geïnteresseerd zijn in de gemiddelde lengte van volwassen Nederlandse vrouwen. Om hiervan een beeld te krijgen, kun je een steekproef nemen uit alle Nederlandse vrouwen en van ieder van hen de lengte meten.

Hieruit blijkt dat de gemiddelde lengte van de vrouwen in de steekproef 1.65m is. Dan is je beste inschatting van het populatiegemiddelde, de gemiddelde lengte van alle volwassen Nederlandse vrouwen, precies dit gemiddelde van 1.65m. Deze schatting wordt een puntschatter genoemd. Een puntschatter is één getal, gebaseerd op één streekproef. Het nadeel van een puntschatter is dat het niks zegt over de nauwkeurigheid van die schatting. Ligt het populatiegemiddelde wel dicht bij het gemiddelde van de steekproef?

Betrouwbaarheidsinterval

Precies om die reden geven onderzoekers vaak een betrouwbaarheidsinterval. Dit is een interval om de puntschatter heen en geeft aan hoe nauwkeurig de puntschatter is. Vaak is dat een 95 procent-betrouwbaarheidsinterval. Lezers van het onderzoek denken vaak dat dit betekent dat de onderzoeker met 95 procent zekerheid kan zeggen dat de schatting klopt. Ofwel, dat het 95 procent zeker is dat de gemiddelde lengte van Nederlandse vrouwen 1.65 meter is. Maar eigenlijk betekent het iets anders. Namelijk dat, als we heel veel steekproeven zouden nemen, in 95 procent van die steekproeven het populatiegemiddelde binnen het betrouwbaarheidsinterval ligt.

Volg je het nog? Mogelijk niet, en dat is ook niet gek. De precieze interpretatie is erg ingewikkeld en wordt helaas ook vaak door onderzoekers fout gedaan. Laten we daarom niet te veel focussen op de precieze interpretatie, maar meer op wat een betrouwbaarheidsinterval je kan vertellen over een puntschatter.

Nauwkeurigheid

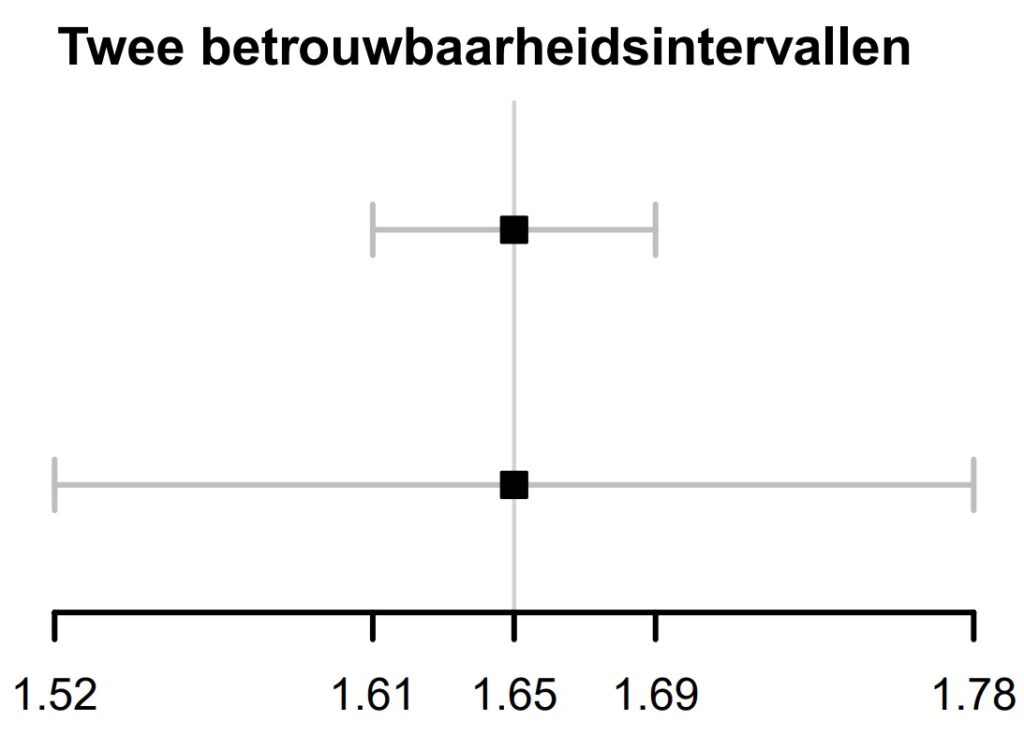
Eigenlijk is vooral de breedte van het betrouwbaarheidsinterval belangrijk. Deze geeft namelijk de nauwkeurigheid van je puntschatter aan. Kijken we weer naar het voorbeeld over de lengte van vrouwen, waarbij de puntschatter 1.65m was, dan zou een betrouwbaarheidsinterval van 1.61m – 1.69m aangeven dat de puntschatter heel nauwkeurig is. Er is maar weinig speling. Bij een interval van 1.52m – 1.78m is de onnauwkeurigheid veel groter. De figuur hieronder geeft je een idee van het verschil.

De grootte van de steekproef en de variatie

Maar waar hangt de breedte van het interval dan vanaf? Twee factoren hebben veel invloed: de grootte van je steekproef en de variatie binnen de populatie.

Hoe groter je steekproef, dus van hoe meer vrouwen je de lengte meet, des te smaller je betrouwbaarheidsinterval. Want hoe meer informatie je verzamelt, hoe meer je over de populatie in het algemeen weet. Denk maar eens in: de gemiddelde lengte over 10.000 vrouwen zegt natuurlijk veel meer over de lengte van vrouwen in het algemeen dan de gemiddelde lengte over maar 100 vrouwen. Hoe meer verzamelde data, hoe nauwkeuriger je puntschatter, en dus hoe smaller het betrouwbaarheidsinterval.

Verder hangt het betrouwbaarheidsinterval ook af van de variatie in de populatie. Als er bijvoorbeeld weinig verschil zit in de lengte van volwassen Nederlandse vrouwen, dan maakt het niet zo veel uit welke vrouwen je selecteert voor de steekproef. De gemiddelden van alle steekproeven liggen dan erg dicht bij elkaar, omdat de lengten van de vrouwen in elke steekproef op elkaar lijken. Maar hoe groter de verschillen in die populatie, hoe onzekerder de schatting uit een steekproef.

In het filmpje hieronder worden beide factoren nog eens uitgelegd (in het Engels) met een voorbeeld over het gewicht van appels.

Waar komt dat wantrouwen vandaan?

Nu we wat meer weten over puntschatter en betrouwbaarheidsintervallen, kunnen we terug naar het wantrouwen dat veroorzaakt wordt door betrouwbaarheidsintervallen.

Als een onderzoeksresultaat wordt gegeven door middel van een betrouwbaarheidsinterval, dan lijkt het alsof een onderzoeker niet zo zeker is van zijn resultaat. Als uit onderzoek blijkt dat ‘de gemiddeld lengte van Nederlandse vrouwen 1.61m – 1.69m is’, dan lijkt dit op een vrij grove schatting. Terwijl de uitspraak ‘de gemiddeld lengte van Nederlandse vrouwen is 1.65m’ heel precies oogt. Je zou dus kunnen denken dat het eerste onderzoeksresultaat aangeeft dat er veel onzekerheid is in het onderzoek. Maar eigenlijk geeft de puntschatter in de tweede uitspraak eerder een vals gevoel van precisie. We kunnen zo’n uitspraak eigenlijk alleen doen als we alle Nederlandse vrouwen hebben opgemeten. Want alleen dan weten we echt het exacte gemiddelde.

Eerlijk zijn over (on)nauwkeurigheid

Als laatste is het goed om te weten dat niet alle waardes in een betrouwbaarheidsinterval even waarschijnlijk zijn. De puntschatter ligt namelijk waarschijnlijk het dichtst bij het populatiegemiddelde. En hoe meer je naar de uiteindes van een betrouwbaarheidsinterval gaat, hoe kleiner de kans dat het echte gemiddelde die waarde heeft. Kijk nog maar een keer naar de grafiek hierboven. De puntschatter is dus het belangrijkste, maar het betrouwbaarheidsinterval is nodig om een idee te geven van de nauwkeurigheid.

Onzekerheid is helaas een onderdeel van onderzoek. We kunnen daarom maar beter eerlijk zijn over de (on)nauwkeurigheid. Onnauwkeurigheden in een onderzoek benoemen, zou daarom moeten worden gestimuleerd. Ze moeten in ieder geval zeker geen reden zijn om een onderzoeksresultaat weg te wuiven.