Forensische statistiek: van bewijs naar overtuiging

Waar denk je het eerst aan bij forensisch onderzoek? Misschien zie je mensen in witte pakken op een plaats delict voor je, die sporen fotograferen en veiligstellen. Of misschien denk je aan een stap verder in het proces, en zie je iemand een onbekende stof analyseren in een lab, of twee vingersporen met elkaar vergelijken. Waar de meeste mensen waarschijnlijk niet direct aan denken, maar wat wel een belangrijke rol speelt in bijna elk onderdeel van forensisch onderzoek, is forensische statistiek.

Statistiek is onmisbaar in forensisch onderzoek, omdat de vragen die door de politie of rechter gesteld worden bijna nooit met een volmondig ja of nee te beantwoorden zijn. Als een schoenspoor op een plaats delict overeenkomt met een schoenspoor van een verdachte, betekent dat niet automatisch dat dit schoenspoor achtergelaten is door de schoen van de verdachte. Er zijn immers nog meer mensen met deze schoen.

Die kans is van allerlei factoren afhankelijk. Hoeveel paren van deze schoenen zijn er in omloop, hoe zeldzaam is de schoenmaat, en zijn er misschien unieke sporen te zien door slijtage of beschadiging die deze kans beïnvloeden? Bij het Nederlands Forensisch Instituut houden statistici zich bezig met dit soort vragen, maar ook deskundigen in andere vakgebieden maken veel gebruik van statistiek.

Bayesiaanse analyse
Bij het rapporteren van waarschijnlijkheden maakt het NFI gebruik van het Bayesiaanse framework. Een Bayesiaanse analyse (pdf download) bestaat uit drie componenten: een a-priori kansverhouding (odds), een likelihood ratio, en een a-posteriori kansverhouding. De a-posteriori kansverhouding wordt verkregen door de a-priori kansverhouding te vermenigvuldigen met de likelihood ratio (LR). Intuïtief gezegd: je begint met een bepaalde mate van overtuiging dat een bepaalde bewering klopt, bijvoorbeeld dat het schoenspoor is achtergelaten door de verdachte.

De likelihood ratio is een maat voor de bewijskracht van de schoenspoormatch. Door de initiële mate van overtuiging (a-priori) te combineren met de invloed van de observaties (LR), verkrijgt men een nieuwe mate van overtuiging (a-posteriori) dat het schoenspoor van de verdachte afkomstig is.

Moord op een cruiseschip
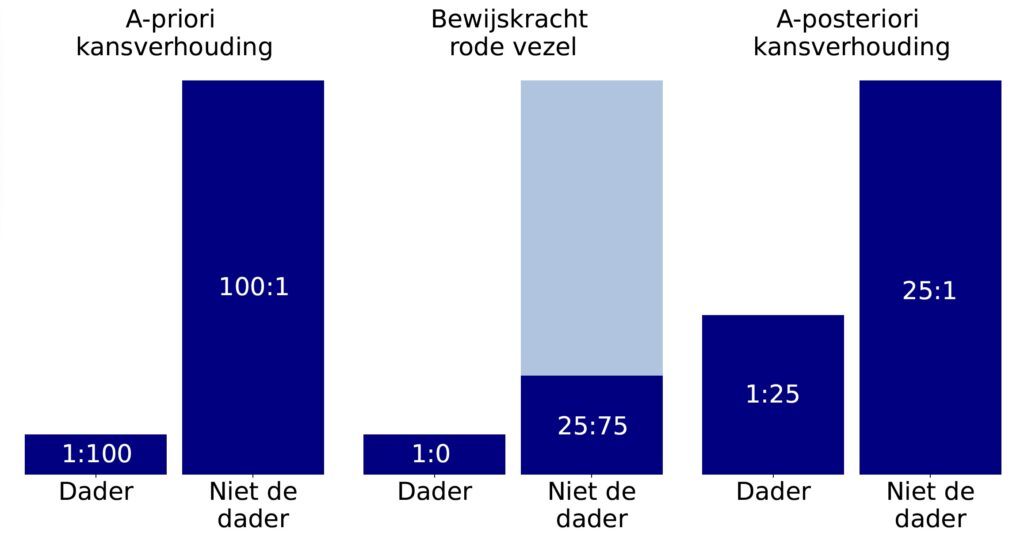
Een simpel forensisch voorbeeld is deze fictieve situatie van een moord op een cruiseschip. Daarbij is zeker dat de dader zich op de boot bevond; er is dus een gesloten populatie van verdachten. Naast het slachtoffer en een verdachte waren er 100 andere mensen aanwezig op de boot. Zonder enig bewijs in beschouwing te nemen, is de a-priori kansverhouding dat deze verdachte ook de dader is, gelijk aan 1:100. Deze a-priori kansverhouding is hetzelfde voor alle aanwezigen op het schip.

Gelukkig is er bewijs gevonden op de plaats delict: een rode vezel, waarvan wordt aangenomen dat deze afkomstig is van de kleding van de dader. De verdachte heeft een rood kledingstuk waarvan de vezel afkomstig zou kunnen zijn. Maar nog 25 andere mensen op de boot hebben ook zo’n kledingstuk. Met deze informatie kan de likelihood ratio tussen twee hypothesen berekend worden, namelijk de hypothese van de aanklager (“De rode vezel is afkomstig van het kledingstuk van de verdachte”) en de hypothese van de verdediging (“De rode vezel is afkomstig van een kledingstuk van iemand anders dan de verdachte”). Voor beide hypotheses wordt berekend wat de kans op de match tussen de vezel en de trui van de verdachte, gegeven dat de hypothese waar is.

Bewijskracht
Stel de eerste hypothese is waar, en de rode vezel is inderdaad afkomstig van het kledingstuk van de verdachte. Dan is de kans dat er een match geobserveerd wordt tussen de rode vezel en dit kledingstuk gelijk aan 1. Stel nu dat de tweede hypothese waar is, en de vezel is afkomstig van het kledingstuk van iemand anders. Van de 100 andere mensen op de boot hebben 25 een passend kledingstuk, dus is de kans dat de vezel matcht wanneer een willekeurige andere opvarende de dader is, 0.25.

De verhouding tussen deze twee kansen is de likelihood ratio, de bewijskracht van de rode vezel. In dit geval is de LR gelijk aan 1/0.25 = 4. Met andere woorden: de match tussen de rode vezel en het kledingstuk van de verdachte is vier keer waarschijnlijker wanneer de verdachte de dader is, dan wanneer iemand anders de dader is. Om nu de kans te berekenen dat de verdachte de dader is, moet de a-priori kansverhouding vermenigvuldigd worden met de LR. Dit geeft een a-posteriori kansverhouding van 1:100 * 4 = 1:25, wat overeenkomt met een kans van ongeveer 3,8%.

Uiteraard is dit in de praktijk een stuk lastiger dan in dit voorbeeld. Op deze boot was de a-priori kansverhouding makkelijk te berekenen, omdat zeker was dat er maar 101 mensen de mogelijkheid hadden de moord te plegen. Bij een echte moordzaak is het veel moeilijker de a-priori kansverhouding te geven, omdat er niet direct een beperkte groep verdachten bestaat waarvan er één zeker de dader is. De populatie die deskundigen gebruiken in de hypothese van de verdediging, hangt van veel factoren af. Hier zal ik in een latere blogpost naar kijken.

Deskundigheid
Goed om te weten is dat deskundigen bij het NFI over het algemeen enkel een likelihood ratio rapporteren, en niet zullen spreken over de a-priori of a-posteriori kansverhoudingen. Dit is het domein van de rechter. Een deskundige rapporteert alleen over zijn specifieke deskundigheid, in de vorm van een LR: hoeveel waarschijnlijker is het observeren van dit bewijs onder de hypothese van de aanklager, versus die van de verdediging?

De grootte van de LR die gerapporteerd wordt, is sterk afhankelijk van het deskundigheidsgebied. Een toevallige match op een DNA-spoor van goede kwaliteit is veel zeldzamer dan een toevallige match met een rode vezel in dit voorbeeld. De LRs die bij DNA-bewijs horen zijn vaak boven de 100.000. Als naast de rode vezel ook een DNA-spoor was gevonden met een LR van 100.000, zou de a-posteriori kansverhouding dat de verdachte de dader is gelijk zijn aan 1:100 * 4 * 100.000 = 4000:1*, wat overeenkomt met een kans van ongeveer 99,975%. Een stuk overtuigender dan de 3.8% zonder het DNA-spoor.

Forensische statistiek is complex en fascinerend. Verkeerde toepassing ervan heeft, zelfs in Nederland, geleid tot onterechte veroordelingen, bijvoorbeeld in de zaak-Lucia de B. Dat geeft aan hoe belangrijk het is dat forensische statistiek bestaat en zich blijft ontwikkelen. De komende tijd laat ik je graag meer zien van dit mooie vakgebied. Volgende keer het antwoord op de vraag: waarom kunnen we niet de kans berekenen dat het dodelijke schot is afgevuurd met het wapen van de verdachte?

*Voetnoot: het vermenigvuldigen van LRs om bewijs te combineren is alleen onder bepaalde omstandigheden mogelijk, en in de praktijk is combineren vaak complexer.