Lootjes trekken met een grote groep: onbegonnen werk?

De feestdagen komen er weer aan. Voor menig kind misschien wel de spannendste tijd van het jaar. Wat zullen zij in hun schoentje krijgen van de Sint? Voor volwassenen is dit misschien net zo spannend: wie trekken zij met hun lootje voor de surprises? Als jullie het lootjes trekken, net als ik, op de traditionele manier doen, zullen jullie ongetwijfeld herkennen dat dit soms wel erg lang duurt.

Het komt vrij vaak voor dat iemand zichzelf trekt en het hele circus van voor af aan moet beginnen. Misschien dat grote families niet meer durven om met de hand te loten, maar een computer laten bepalen wie jij krijgt. Wees niet bang, het duurt gemiddeld drie rondes voordat niemand zichzelf loot, of je nu met 5 of 1000 personen bent. Hoe dat zit, leg ik je in deze blog uit.

Klein beginnen
Laten we beginnen met het meest simpele geval: twee personen, Ada en Bert, trekken lootjes. In dit geval zijn er maar twee mogelijkheden: 1) Ada loot Ada en Bert loot Bert, of 2) Ada loot Bert en Bert loot Ada. In scenario 1 moeten ze opnieuw beginnen en in scenario 2 is het spel voorbij. Beide scenario’s zijn net zo waarschijnlijk, dus de kans dat dit in één keer goed gaat, is 50%. Het wordt wel een saaie sinterklaasavond zo, dus laten we iemand extra erbij halen.

Ada en Bert nodigen Chris uit om ook mee te doen met lootjes trekken. Met 3 personen wordt het al wat ingewikkelder om te berekenen wat de kans is dat dit in één keer goed gaat. Er zijn 6 mogelijke uitkomsten: Ada, Bert, en Chris (ABC) loten respectievelijk: ABC, ACB, BAC, BCA, CAB, of CBA. In 4 van de 6 gevallen (ABC, ACB, BAC, CBA) heeft tenminste 1 iemand henzelf getrokken, in 2 van de 6 gevallen gaat dit goed.

Grotere groepen
Voor meer personen wordt dit wel erg onoverzichtelijk om alles uit te schrijven. Het figuur hieronder laat zien wat de kans is dat dit goed gaat. Hieruit blijkt dat de kans niet kleiner is naarmate het aantal personen in je groep groeit. Sterker nog, vanaf een groepsgrootte van 5 en meer is de kans nagenoeg gelijk dat niemand zichzelf loot.

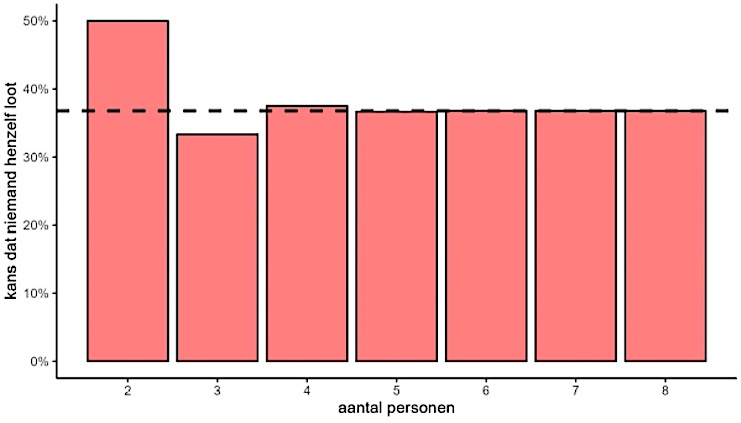
Er zijn namelijk twee factoren die elkaar balanceren. Aan de ene kant betekent een grotere groep een kleinere kans dat je je eigen lootje pakt, Aan de andere kant betekent een grote groep dat er meer mensen zijn die zichzelf kunnen loten. Dit wiskundige fenomeen wordt ook wel het derangement genoemd. Voor een groep van vijf of meer personen is de kans zo’n 36,8% (de zwarte stippellijn) dat niemand zichzelf loot. Voor de fanatiekelingen onder ons: de exacte kans dat niemand zichzelf loot met n personen is.

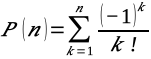
Van één naar meerdere rondes
Nu hebben we alle informatie om te berekenen hoeveel rondes het gemiddeld duurt totdat niemand zichzelf loot. We weten al dat de kans ongeveer 36.8% is dat niemand zichzelf loot in ronde 1. De kans dat niemand zichzelf in ronde 2 loot kunnen we berekenen door de kans dat er wél iemand zichzelf in ronde 1 loot (100% – 32.8% = 63.2%) te vermenigvuldigen met de kans dat er niemand in ronde 2 zichzelf loot (32.8%), wat uitkomt op ongeveer 23.3%. Dit trucje kunnen we voor iedere ronde herhalen. Dit wordt ook wel de geometrische verdeling genoemd.

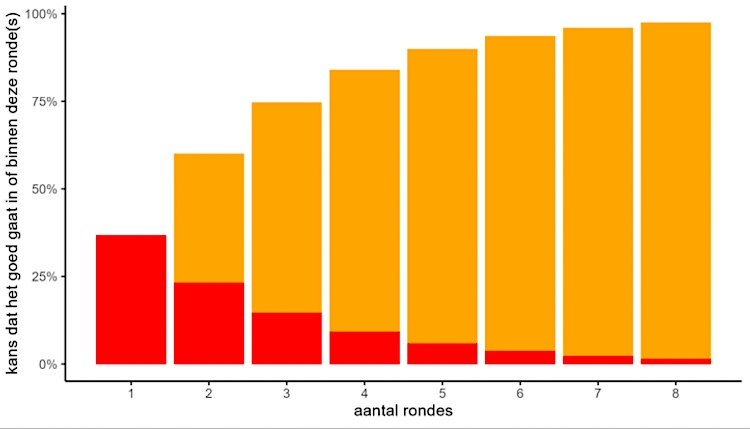
In het onderstaande figuur zie je in het oranje de kans dat het loten binnen n rondes goed gaat en in het rood de kans dat het in ronde n beslist wordt. Het lootjes trekken wordt het vaakst in ronde 1 beslist. In 90% van de gevallen duurt het maximaal 5 ronden totdat niemand zichzelf heeft geloot. Gemiddeld duurt het ongeveer 2.81 ronden totdat niemand zichzelf heeft geloot. Voor wiskundigen is dit een bijzonder getal: het is Eulers nummer e en heeft, net als het getal pi, vele bijzondere toepassingen.

Het getal e
Misschien herken je de constante e van de middelbare school. Het getal e is bijzonder, omdat zowel de afgeleide (helling van de functie) als de integraal (oppervlakte onder de functie) van

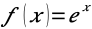
in alle gevallen

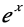
is. Het getal komt voornamelijk voor in toepassingen met exponentiële groei.

De formule voor de normaalverdeling, één van de belangrijkste verdelingen in de statistiek, bevat e als grondgetal. Ook in de financiële wereld komt het getal e voor als je rekent met samengestelde rente.

Het getal is namelijk te benaderen met de formule

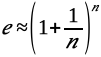
voor grote waarde van n. Ook in de kansberekening komt e vaak voor: de zwarte stippellijn in het eerste figuur heeft de waarde 36.8%, wat niet toevallig 1/e is.

Kortom, ga lekker ouderwets lootjes met de familie en vrienden trekken. Het duurt echt niet zo lang als je denkt (ongeveer 3 rondes), ook al zijn jullie met veel. De kans is notabene het grootst dat het in één keer goed gaat. Fijne feestdagen!

Hoofdfoto: Ylanite Koppens, via Pexels