De optimale route naar een touchdown in American Football

Een verrassende toepassing van wiskunde. Steijn Heijerman, student Toegepaste Wiskunde aan de Hogeschool van Amsterdam, heeft een methode bedacht om de optimale route te bepalen naar de endzone in American Football. De endzone is het gebied achter de doellijn van de tegenstander. Hij studeerde op dat onderwerp af bij Beyond Sports, een datavisualisatiebedrijf.

De opkomst van data en AI gaat ook aan de sportwereld niet voorbij. Het bedrijf Beyond Sports gebruikt wiskundige methodes om sportwedstrijden op nieuwe manieren te visualiseren. In het voetbal beschikt het bedrijf onder andere over sensordata van spelers en de bal. Zo kunnen ze de wedstrijd real time simuleren in de stijl van de film Toy Story. Ook kunnen ze tijdens een wedstrijd het beeld laten veranderen van perspectief. Die succesvolle vrije trap kun je dan niet alleen zien vanuit de hoek van de camera op het veld, maar ook door de ogen van de keeper.

Het kortstepad-probleem
Heijerman ging aan de slag met een andere sport: American Football. Een speler kan in deze sport op meerdere manieren scoren. Eén manier is via een touchdown. Daarvoor brengt een speler de bal in de endzone, het gebied achter de doellijn, van de tegenstander. Maar hoe kan hij het beste lopen, afhankelijk van de positie en snelheid van de tegenstanders en zijn eigen teamleden? Dit wilde Beyond Sports weten, zodat sportanalisten die informatie kunnen gebruiken als ze een wedstrijd van commentaar voorzien.

Steijn Heijerman benaderde deze opdracht met twee elementen uit de wiskunde. Het kortstepad-probleem en het concept van de zogenoemde player influece.

Bij het kortstepad-probleem zoek je het kortste pad tussen een beginpunt en een eindpunt. Tussen deze twee punten liggen verschillende knooppunten. De afstanden tussen de knooppunten zijn bekend, en er zijn meerdere routes mogelijk. Het kan gaan om een fysieke afstand, in meters, maar bijvoorbeeld ook om de laagste kosten om goederen te vervoeren, of in de kortste tijd. In de figuur hieronder is een voorbeeld te zien. De kortste afstand tussen beginpunt A en eindpunt G gaat via C, E, B en D.

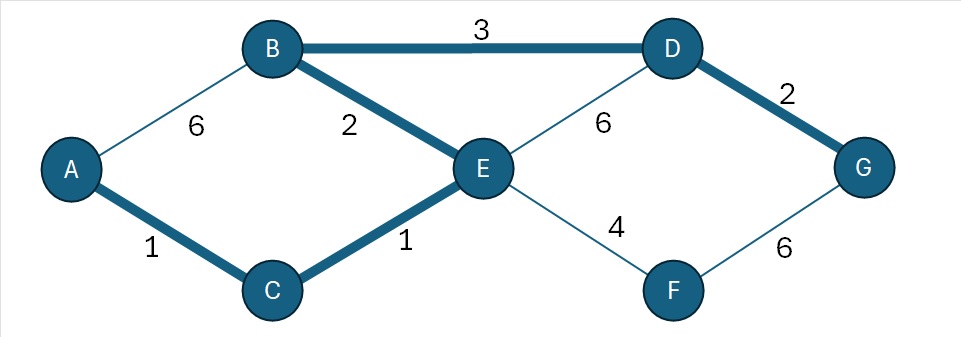
In dit voorbeeld kun je zelf nog wel achter de kortste route komen. Maar als het aantal knooppunten toeneemt, is een andere aanpak nodig. Het algoritme van Dijkstra is een veelgebruikte methode om zo’n probleem op te lossen. Het geeft een stap-voor-stap instructie hoe je de kortste route vindt. En die taak kan een computer uitstekend op zich nemen. Google Maps gebruikt soortgelijke algoritmes om te bepalen hoe je het snelst op je gewenste bestemming komt.

Veldcontrole
Het tweede element dat hij gebruikte, is een wiskundige manier om de invloed van een speler op het voetbalveld te bepalen. Die player influence houdt rekening met de positie van een speler, de looprichting, zijn snelheid, en de positie van de bal. Bijvoorbeeld: hoe dichter een speler bij de bal is, of hoe meer hij in de richting van de bal beweegt, des te hoger zijn score. Voor elk punt op het veld kun je zo de veldcontrole van een team berekenen door de invloed van de tegenstanders af te trekken van de invloed van de eigen spelers. Deze maat vertaalde hij voor zijn onderzoek naar American Football. Wil een speler de endzone bereiken, dan moet hij plekken vermijden waar de tegenstander veel invloed heeft.

Oplossing: een creatieve aanpassing van afstanden
Deze twee elementen leiden tot een optimale route. Eerst legde hij een raster van 1 bij 1 meter met knooppunten over het American Footballveld (zie hieronder). Vervolgens paste hij de afstand tussen de knooppunten aan, afhankelijk van de veldcontrole. Op plekken waar de tegenstander veel invloed had, vergrootte hij de afstand en verkleinde de afstand op de plekken met weinig invloed. De optimale route naar de endzone is de route met de kortste aangepaste afstand. En die kon hij met behulp van het algoritme van Dijkstra berekenen.

Schematische weergave van het American Football veld, met raster en knooppunten. Het rode en blauwe gebied zijn de endzones van de twee teams. Bron: Scriptie Heijerman.

Resultaat: realistische routes
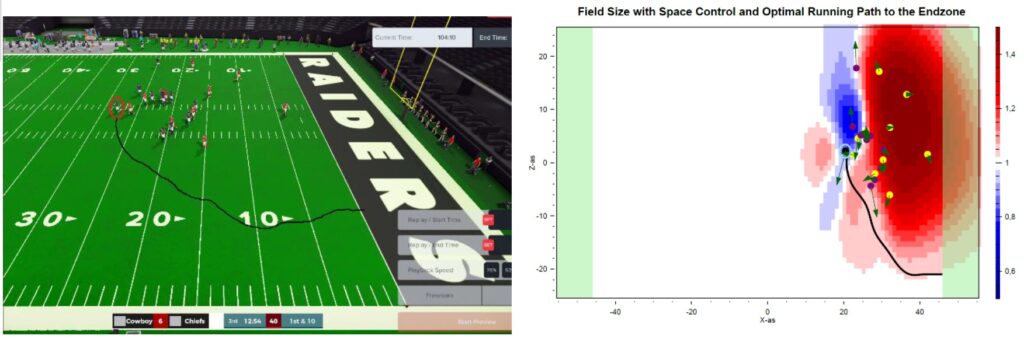
Werkt dit ook in de praktijk? Om dat te bepalen, vergeleek hij de werkelijk gelopen paden met de optimale berekende routes. Hieronder een voorbeeld. Links staat de daadwerkelijk afgelegde route. Rechts de berekende route.

De zwarte stip geeft de locatie van de speler met de bal aan. De rode puntjes zijn medespelers, de gele puntjes de tegenstanders. De pijlen geven aan welke kant iemand op beweegt. In het blauwe gebied heeft het aanvallende team controle. Hoe roder de kleur, hoe hoger juist de invloed van de tegenstander. Het donkerrode gebied moet een speler dus vermijden. De zwarte lijn geeft het berekende optimale pad aan. De speler neemt een omweg om de tegenstander te vermijden, en de route is erg vergelijkbaar met de daadwerkelijk gelopen route. Een prachtig resultaat. De methode geeft realistische uitkomsten en Beyond Sports kan deze gebruiken om de toeschouwer van inzichten te voorzien.

Door op een innovatieve manier een algoritme voor het kortstepad-probleem te combineren met een wiskundige maat voor controle op het veld, kon Steijn optimale looproutes naar de endzone in het American football bepalen. Zijn onderzoek laat zien dat wiskunde breed toepasbaar is. Beyond Sports kan zijn methode gebruiken om de kijker deze sport op een wiskundig onderbouwde manier te laten beleven.

Alle figuren zijn afkomstig uit de scriptie van Steijn Heijerman en zijn met toestemming gebruikt. Je kunt de scriptie hier downloaden:

Hoofdfoto: Joe Calomeni via Pexels