Science is a major gamble. Let’s be explicit how we’re betting.

On June 30th, 2020, the US Food and Drug Administration (FDA) published its guidance document on “Development and Licensure of Vaccines to Prevent Covid-19” (FDA, 2020). This set the goals for any Phase III clinical trial betting on a protective effect of a vaccine against Covid-19. The guidance document advised on the definition of events of confirmed (symptomatic) SARS-CoV-2 infection for the trials to be counting. And in counting those, the document prescribed two things to achieve: (1) at least a vaccine efficacy (VE) of 50% and (2) evidence against a null hypothesis of less than 30% VE (FDA, 2020, p. 14).

What is the purpose of a clinical trial when a statistical analysis is supposed to reject that null hypothesis? The risk of SARS-CoV-2 is random; especially in terms of the infection count per group since participants were randomly assigned to either vaccine or placebo group. So the purpose is to collect evidence that one random model, with limited VE <=30%, is not in good agreement with what we observe in a clinical trial. We can show that by predicting a better random model, with >=50% VE, for which we hope that there is a better agreement. With a competing model we are essentially betting against the null model by making better predictions.

In a recent paper (Ter Schure & Grünwald, 2021) prof. dr. Peter Grünwald and I introduce this statistical thinking for a wide range of statistical problems. In the following, we reinterpret the design for the Covid-19 vaccine trials in the language of betting. We show that the FDA designed a transparent game, that the Pfizer-BioNtech vaccine trial had the odds in its favor and that the winnings – the betting score – are quite an intuitive notion to communicate the remaining uncertainty in such scientific results.

Betting on vaccine and placebo infections

According to the definition of SARS-Cov-2 infections, we start counting once a participant has a confirmed infection after being fully vaccinated for at least a number of days (e.g. 7 days in the Pfizer-BioNTech trial (Polack et al, 2021)). This is also when a (virtual) bet could start. Each new infection carries evidence that we express by a betting score. We make a (virtual) investment on one of the two outcomes: either the next infection occurs in the vaccine group or it occurs in the placebo group. If there is no effect of the vaccine whatsoever, for balanced randomization* the infected participant has 0.5 a chance to be vaccinated and 0.5 a chance to be a placebo.

Yet, following the FDA, we do not only want to rule out an ineffective vaccine but also reject the hypothesis that the vaccine has an effect that is too small—set as the null hypothesis of (at most) 30% VE. In that case, each newly observed infection has a slightly smaller chance to be a vaccinated participant. That probability to be in the vaccine group is 0.41 since each placebo group member has a 100% risk of Covid-19 and a vaccine group member has 100 – 30 = 70% of the risk, which is a fraction 0.41 of the total risk (70/(100 + 70)). So if the VE is too small to be of interest we expect (at least) a fraction 0.41 of Covid-19 infections to occur in the vaccine group and (at most) 0.59 in placebo.

How do we bet against that and win if the vaccine has a much larger protective effect?

We are betting against the probability 0.41 of the next Covid-19 infection to occur in the vaccine group. If this probability actually is that large (the vaccine is not very protective; the null hypothesis) we do not want the game to be favorable under any strategy, just like the casino does not want any gambler to earn a salary playing the roulette wheel. On the other hand, we are betting in favor of a much smaller probability for the vaccine group. If this probability is smaller (the vaccine is protective; the alternative hypothesis) we do want to win money, just like a professional poker player who makes a salary out of gambling well.

We use the betting scores to decide whether the vaccine is a real deal-breaker (the scores behave like the salary of a professional poker player) or whether it is not effective enough (the scores behave like anyone playing the roulette wheel). To ensure that our betting scores can show either case, we first design the game such that it is fair—under the null hypothesis—and then optimize playing the game with a strategy that is profitable—under the alternative.

Designing a fair game under the null hypothesis

Consider gambling at the roulette table where the vaccine trial analogy is like betting on red (vaccine) or black (placebo). Betting correctly doubles your investment, betting incorrectly loses everything you risked. Assuming no house edge and an initial €100 you do not expect to increase your investment since you have 0.5 a chance of doubling (2 x €100) and 0.5 a chance of losing all (0 x €100). Whether you bet everything on black or red, in expectation the betting score after one round is (0.5 x 2 + 0.5 x 0) x €100, which is the initial investment of €100.

To achieve the same thing betting against the 0.41:0.59 probabilities instead of 0.5:0.5, your investment needs to multiply by 2.4 (1/0.41) for vaccine and 1.7 (1/0.59) for placebo. If you bet everything on vaccine you have a 0.41 chance of multiplying by 2.4 (2.4 x €100) and 0.59 chance of losing all (0 x €100) and if you bet everything on placebo you have a 0.59 chance of multiplying by 1.7 (1.7 x €100) and 0.41 chance of losing all (0 x €100). The expected betting score after one round is again the initial investment for both: (0.41 x 1/0.41 + 0.59 x 0) x €100 and (0.59 x 1/0.59 + 0.41x 0) x €100.

Hence, at either the roulette table or in this FDA game, by design the game is fair and not favorable to us. After all, if our observed infections land on the vaccine and control with the probabilities 0.41:0.59—like a spin of the roulette wheel on black and red with 0.5:0.5—we do not expect to claim an effective vaccine.

Optimize playing the game under the alternative hypothesis

How do we win as fast and as much as possible if our observed infections do not behave like a roulette wheel? It has been known since the work of Kelly (1956) and Breiman (1974) that the best way to increase your capital in the long run is to not bet all your (virtual) investment €100 on one of the two possible outcomes (red/vaccine or black/placebo) but to divide it based on the odds that make the game favorable to you. So our focus needs to be on the minimal VE of 50% from the FDA guidance. In the scenario of 50% VE, the probability that the next Covid-19 case is in the vaccine group is 1/3: if we set the risk of Covid-19 for a placebo group member to 100%, a vaccine group member has 100-50 = 50% of that risk, which is 1/3 of the total risk (50/(100 + 50)). Kelly and Breiman urge us to invest one-third (1/3 x €100) on observing the next infection in the vaccine group and two-thirds (2/3 x €100) on placebo.

Likelihood ratios

If we bet this way we can rewrite our betting scores in terms of a likelihood ratio. We first show this for the red-black roulette game where we double what we had put at risk on either black or red if the spin of the roulette wheel outputs the color we bet on. Just like in our strategy in the FDA game, we put 1/3 x €100 on red and 2/3 x €100 on black, so we win the following if the ball X lands on either red or black:

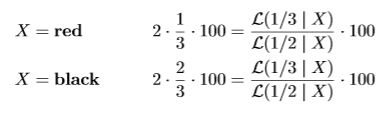
The Bernoulli 1/3-likelihood assigns likelihood 1/3 when is X = red and 2/3 when is X = black. So if our strategy is to invest 1/3- 2/3 in roulette, our payout is our initial investment €100 multiplied by the likelihood ratio, whether X is red or black.

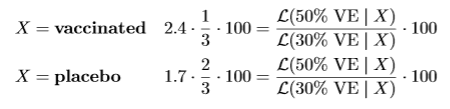
The likelihood for 50% VE assigns likelihood 1/3 when is X = vaccine and 2/3 when is X = placebo. Similarly, the likelihood for 30% VE assigns likelihood 0.41 when is X = vaccine and 0.59 when is X = placebo. Hence if our strategy is to invest 1/3-2/3 in the FDA game, our payout is also our initial investment €100 multiplied by the likelihood ratio, whether X is vaccine or placebo.

Reinvesting over multiple rounds

Let’s assume that we start with an initial (virtual) investment of €1 instead of €100. At the first observation we bet €0.33 on vaccine and €0.66 on placebo. After we observe an infection in the placebo group we lose our €0.33 bet on vaccine and multiply our €0.66 on placebo by 1.7 to €1.13. The likelihood ratio between our 30% VE alternative hypothesis and our 50% VE null hypothesis is also 1.13, so multiplying our initial investment of €1 into €1.13. On the other hand, if we observe the infection in the vaccine group we lose our €0.66 bet on a placebo infection and multiply our €0.33 on vaccine by 2.4 to €0.81. The likelihood ratio of a vaccine infection multiplies our investment by 0.81. After each observed infection we reinvest what we have left in the new bet, so multiply that with the next likelihood ratio.

A winner

The Pfizer/BioNTech trial observed 8 cases of Covid-19 among participants assigned to receive the vaccine and 162 cases among those assigned to placebo (Polack et al, 2020). By reinvesting, it could report a total betting score of 0.81^8 x 1.13^162 x €1, which is about €118 million (note that 1.13 is really 1.13333 . . .)**. If someone wins that at the poker table, we have good reason to consider her a professional poker player with a favorable strategy, rather than a lucky beginner (Konnikova, 2020).

Statistical testing by betting

As Shafer (2021) puts it: “When statistical tests and conclusions are framed as bets, everyone understands their limitations. Great success in betting against probabilities may be the best evidence we can have that the probabilities are wrong, but everyone understands that such success may be mere luck.”

The roulette example above is due to Peter Grünwald. The exact description here also serves as the introductory example in a paper that extends this reasoning to meta-analysis of clinical trials (Ter Schure & Grünwald, 2021). In this paper – ALL-IN meta-analysis – we argue that honest bets can serve evidence-based medicine by facilitating living systematic reviews and reducing research waste. ALL-IN stands for Anytime, Live and Leading INterim meta-analysis.

* Most Covid-19 vaccine trials randomized large numbers of participants (>20.000 in each group in the Pfizer/BioNTech trial) 50:50 vaccine:placebo such that we can assume that also throughout the trial the participants at risk stayed approximately balanced.

** We can ask: why did the Pfizer/BioNTech trial not declare efficacy sooner? In a later agreement with the FDA in October, the vaccine trials committed to collecting at least two months of safety data for half of the included participants in the trial. So the trial could not stop earlier. This agreement was formalized in the FDA guidance document for Emergency Use Authorization and is still present in the May 2021 version (FDA, 2021, p. 10-11).

References

Leo Breiman. Optimal gambling systems for favorable games. Fourth Berkeley Symposium, 1961.

FDA. Development and Licensure of Vaccines to Prevent COVID-19, 2020. https://www.fda.gov/media/139638/download.

FDA. Emergency Use Authorization for Vaccines to Prevent COVID-19, 2021. https://www.fda.gov/media/142749/download.

J.L. Kelly. A new interpretation of information rate. Bell System Technical Journal, pages 917–926, 1956.

Maria Konnikova. The Biggest Bluff: How I Learned to Pay Attention, Master Myself, and Win. Penguin, 2020.

Fernando P Polack, Stephen J Thomas, Nicholas Kitchin, Judith Absalon, Alejandra Gurtman, Stephen Lockhart, John L Perez, Gonzalo Pérez Marc, Edson D Moreira, Cristiano Zerbini, et al. Safety and efficacy of the bnt162b2 mRNA covid-19 vaccine. New England Journal of Medicine, 2020.

Judith ter Schure & Grünwald. ALL-IN meta-analysis: breathing life into living systematic reviews. arXiv:2109.12141. 2021.

Glenn Shafer. Testing by betting: A strategy for statistical and scientific communication. Journal of the Royal Statistical Society: Series A (Statistics in Society), 184(2):407–431, 2021.

Main image: Roulette Table, Håkan Dahlström on Flickr

---