De Top 2000 voorspellen

De Top 2000. Een welkome ‘trip down memory lane’ in deze toch donkere en ietwat eenzijdige dagen. Mijn muzikale opvoeding vond grotendeels plaats in de late eighties, vroege nineties. En laten die twee decennia nu goed vertegenwoordigd  zijn in de Top 2000: ik vermaak me wel. Als statisticus vraag ik me altijd af hoe goed de ranking te voorspellen is. Totaal nutteloos natuurlijk, maar wel een leuk spelletje met collega nerds. Hieronder laat ik zien hoe je uit de gegevens van afgelopen vijf jaar de Top 2000 van 2021 kunt voorspellen.

De data

Alles begint bij de data, en deze zijn beschikbaar op Wikipedia¹. Gesorteerd op de ranking van 2021, met Queen keurig bovenaan. Inclusief missende waarden, daar schrijven sommige statistici boeken over vol. Grap is dat er in de Top 2000 tabel twee typen missende waardes zijn: één echte, namelijk nummers die nog niet uitgebracht waren in een bepaald jaar, aangegeven met ‘x’ en één ander type: een notering lager dan 2000, aangegeven met een ‘-‘. Gecensureerd noemen we dat. In een geavanceerde analyse moet je hier verschillend mee omgaan. Hier heb ik maar weinig missende waardes, dus ik vervang ze simpelweg door 2001, de eerstvolgende ranking.

Model, deel 1: De uitkomst

We gaan verder met misschien wel het leukste deel van de statistiek: het voorspelmodel opstellen. De uitkomsten zijn de rangen van de liedjes. Nu zijn rangen een beetje lastig. Ten eerste: ze zijn niet onafhankelijk van elkaar, want er kan maar één de nummer 1 zijn natuurlijk. Dit schuiven we even onder het tapijt, en is voor de analyse vermoed ik niet erg essentieel. Ten tweede: ze moeten positief zijn, en geheeltallig. Ik wil een standaard regressieanalyse doen, en deze leent zich hier niet voor. Maar er is een trucje voor: ik transformeer de rangen naar de (half-)normale (Gaussische) schaal. Ik doe dat zo dat nummer 2000 een 0 wordt. Nummer 1 wordt dan 3.48, nummer 100 wordt 1.96, nummer 1000 wordt 0.67, en nummer 2000 wordt dus 0. Een soort score dus. Gelukkig kan ik voor interpretatie altijd terugtransformeren.

Model, deel 2: De mogelijke voorspellers, de variabelen

Het creatieve deel van het modelleerproces. Hieronder het lijstje dat ik gebruikt heb.

1. Met stip: Ranking van vorig jaar, net als de uitkomst ook getransformeerd. Als ik de twee tegen elkaar uitzet in een grafiek blijkt het verband erg lineair te zijn, dus ik hoef hier niets moeilijks mee te doen.
2. Gemiddelde ranking van afgelopen vijf jaar. Consistentie wordt beloond. Als een liedje jonger is dan vijf jaar middel ik alleen over de bekende jaren.
3. Leeftijd van de song. Mijn vader vindt de top 2000 steeds minder leuk, want voor zijn gevoel verdwijnen er steeds meer songs uit de sixties. Ik verwacht niet per se een lineair effect, dus ik groepeer even voor het gemak: 0-10 jaar, 10-30, 30-50, ouder dan 50.
4. Stijgende lijn. Als een liedje de afgelopen jaren aan het stijgen is, is dat wellicht een indicatie voor een nog hogere notering in 2021. Evenzo voor de dalers. Ik gebruik het verschil van de afgelopen twee jaren als voorspeller. Als het liedje twee jaar geleden nog niet was uitgebracht, dan zet ik ik dit verschil op 0, neutraal dus.
5. Sentiment. Een bekend gegeven is dat als een artiest afgelopen jaar overleden is, of een oud liedje extra in het nieuws is geweest vanwege een grote gebeurtenis, dan stijgen de kansen van dit liedje om hoog in de Top 2000 te komen.  Maar oei, sentiment is erg moeilijk voor statistici, want dit is onmogelijk objectief in een model te vangen. Ik heb een subjectieve poging gedaan. Alle liedjes van de Golden Earring die in de afgelopen tien jaar in de top 2000 hebben gestaan markeer ik, en daar voeg ik ‘A whiter shade of pale’ van Procol Harum aan toe. U kent de trieste redenen: de ALS-diagnose bij Earring-gitarist George Kooymans, en de moord op Peter R. de Vries. Van al die liedjes deel ik de voorspelde rang (adhv 1 t/m 4) simpelweg door 3. Dus voorspelt het model 141, dan wordt dit 141/3 = 47. 

Model, deel 3: lineaire regressie

Ik gebruik de moeder der alle statistische modellen: het lineaire regressie model. Waarom moeilijk doen als het makkelijk kan? Ik veronderstel dus een lineair verband tussen de uitkomst (de getransformeerde ranking van dit jaar) en de variabelen. Het mooie van regressie is dat het op een heel natuurlijke manier rekening houdt met de correlatie tussen de variabelen, dit noemen we ook wel collineariteit. Want de effecten van de ranking vorig jaar en gemiddelde ranking afgelopen vijf jaar kun je natuurlijk niet los zien van elkaar.

Resultaten

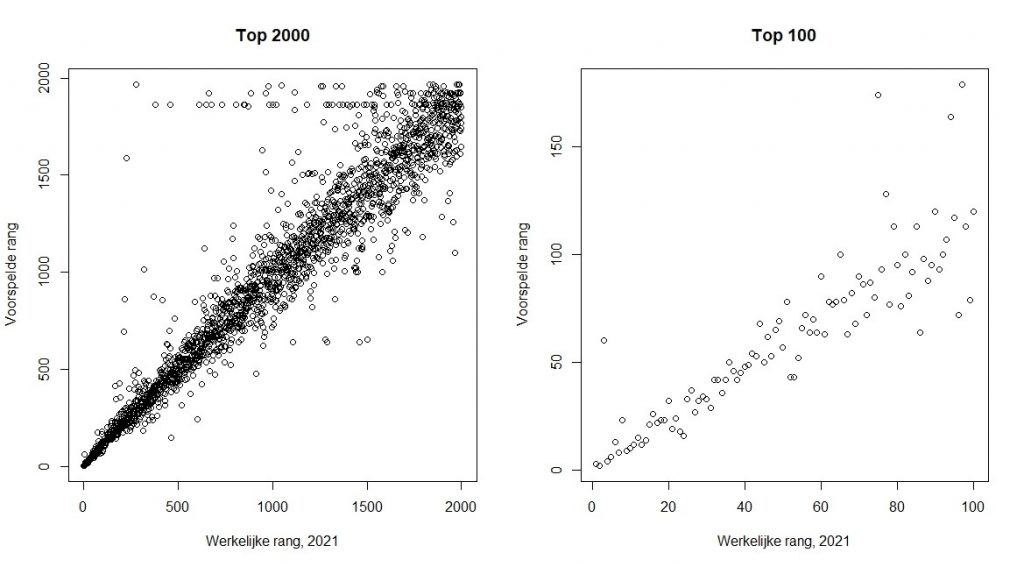
Ik beoordeel de resultaten op twee manieren. Allereerst: de R² waarde. Deze drukt uit welk deel van de variatie in de uitkomst wordt verklaard door de variabelen. Hier zit het wel goed mee: deze is maar liefst 0.936. Wauw. Ten tweede: rangcorrelatie tussen voorspelde ranking en de echte ranking. Dus:  ik bouw het voorspelmodel op basis van de 2020 data, gebruik dit model om de rankings te voorspellen voor 2021, en correleer deze met de echte rangen. Ook deze is geweldig: 0.944, dus erg dichtbij het maximum van 1. Het figuur onder laat deze goede correlatie ook zien. Minder goed voorspelde songs zijn bijvoorbeeld een relatieve nieuwkomer als “Guaranteed” van Eddie Vedder (links; op 227) en, ondanks mijn correctie, “A Whiter Shade of Pale” (rechts; op 3).

Maar…

Niet slecht, toch? Maar nu de teleurstelling. Het allersimpelste model, met alleen de ranking van vorig jaar meegenomen, is vrijwel net zo goed: R² = 0.929, correlatie = 0.941. Ai. Maar dit geeft niet. Zolang je het moeilijkere model niet hebt geprobeerd, weet je ook niet of het beter is. Let op: dit zegt niet dat de andere variabelen op zichzelf niet voorspellend zijn. Ze voegen alleen niks toe. Ik zie dit ook vaak bij medische voorspelproblemen: allerlei nieuwe variabelen voegen betreurend weinig toe aan de bekende variabelen. Is ook een belangrijke boodschap, hoewel dat helaas vaak niet zo wordt gezien. Maar wat betreft de Top 2000: geniet ervan, en ik beloof u: volgend jaar kom ik wat eerder met mijn voorspelling.

Ps. Kunt u het beter? De eerste die mij een oplossing stuurt met een (Spearman) rangcorrelatie > 0.96 stuur ik het boekje: “The lady tasting tea”. Alle data en mijn R-script (incl. data-voorbewerking) vindt u hier.

Noten

¹Dank aan Fabian Feijen voor instructies op linkedin over hoe de wikipedia lijst naar Excel om te zetten.

²Plaatje: commons.wikimedia.org.