Wat wiskunde, dobbelstenen en de Monopoly-gevangenis met elkaar gemeen hebben

De originele post is geschreven door Carien Leushuis van CQM en is hier te vinden

Bij ons thuis verschijnt er regelmatig een gezelschapsspel op de keukentafel. Van het aanleggen van spoorverbindingen tussen steden tijdens Ticket to Ride tot het maken van een lapjesdeken met Patchwork. De spellenkast is door de jaren heen enorm gegroeid. Toch gaat er nog altijd niks boven een ouderwets en gezellig avondje Monopoly. Tijdens het spel heeft ieder van ons gezin zijn of haar eigen strategie en eigenaardigheden. Waar Sophie haar geluk op de proef stelt en zoveel mogelijk kans- en algemene fondskaarten probeert te bemachtigen, koopt Max met zijn kruiwagen strategisch alle stations en nutsbedrijven op. Ondertussen beweegt Evy zich onverminderd voort over het bord en laat alles dat ze onderweg tegenkomt verdwijnen in haar Hoge Hoed. Maar hoe zorg je ervoor dat je aan het einde van de avond als miljonair naar huis gaat? In deze post laten we zien hoe je met een beetje hulp van wiskunde je winstkansen bij Monopoly een handje kunt helpen. Zonder vals te hoeven spelen 😉

Kansrekenen in de praktijk

Monopoly is een bordspel waarin spelers vastgoed kopen en verkopen en elkaar huur in rekening brengen. Spelers verplaatsen hun pionnen over het spelbord door met twee zeszijdige dobbelstenen te gooien. Met deze dobbelstenen kun je alles gooien van een 2 (dubbel één) tot 12 (dubbel zes). Echter zijn sommige uitkomsten waarschijnlijker dan andere. Dit noemen we in de wiskunde ook wel stochastiek of variatie. Stochastiek komen we tegen bij veel van onze klanten, het leven laat zich nu eenmaal leiden door toeval en onzekerheid, geluk of pech. Denk aan beschuit met muisjes: wat is de verwachte datum dat je het kleine wondertje mag verwelkomen? Of aan het weer: wat is de kans dat er komende week nog sneeuwval komt of kunnen de winterbanden dan toch eindelijk de kast in en plaatsmaken voor zomerbanden? En wat denk je van in- en uitstaptijden van passagiers? Of het beheren van voorraad in een onzekere markt?

Kansrekenen met dobbelstenen 

In Monopoly bepaalt stochastiek, ofwel het gooien van een tweetal dobbelstenen, hoe een speler zich voortbeweegt over het spelbord en daarmee de kans om een vakje op het spelbord te bezoeken. Hoe gaat dit in zijn werk? Wanneer we één keer met een tweetal dobbelstenen gooien dan hebben we de grootste kans dat we een 7 gooien. Er zijn namelijk een zestal mogelijke combinaties: (1,6), (2,4), (3,4), (4,3), (5,2) en (6,1). Het getal drie kunnen we bijvoorbeeld slechts op twee manieren verkrijgen (1,2) of (2,1). Deze informatie kunnen we samenvatten in een zogenoemde kansverdeling, zie onderstaande figuur. 

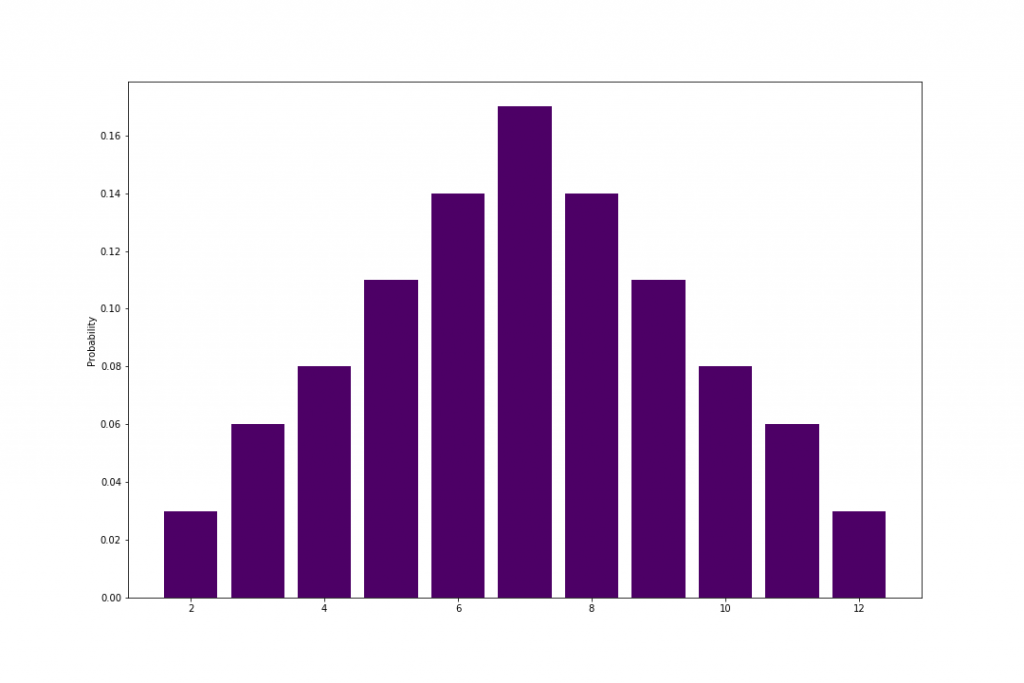
Zoals bovenstaande figuur laat zien hebben niet alle uitkomsten van een dobbelsteen dezelfde kans. Is dit al de sleutel tot succes? Zorgt dit weetje er al voor dat jij de miljardair wordt en niet de zwerver die huur betaalt met zijn laatste biljet? Nee, helaas, Monopoly zou erg saai zijn wanneer de uitkomst van het spel enkel afhangt van de worpen die er met de dobbelstenen worden gemaakt. Er houden zich meerdere addertjes onder het gras verborgen die zorgen voor een leuke twist in het spel!

Ga direct naar de gevangenis

Eén van deze verborgen addertjes zijn de kans- en algemene fondskaarten waar Sophie haar ticket naar Las Vegas tussen probeert te vinden. De meeste van deze kaarten vragen je een boete te betalen of belonen je voor het winnen van een kruiswoordpuzzel. Echter zijn er ook kaarten die je naar een andere plek op het spelbord sturen, waardoor sommige vakjes op het spelbord een extra grote kans hebben om te worden bezocht. Een ander verborgen addertje is het dubbel gooien van de dobbelstenen. Wanneer we dubbel gooien mogen we nogmaals gooien. Echter, gooi je driemaal achter elkaar dubbel, dan vlieg je zonder pardon de gevangenis in. Hoe beïnvloeden deze factoren de bezoekkans van een vakje op het spelbord? Wat is bijvoorbeeld de kans dat je het Neude in Utrecht zal bezoeken om vervolgens weer verder te dobbelen? En verschilt dit van het aantal keren dat je de blauwe Kalverstraat in Amsterdam torenhoge huren moet betalen? Of in de gevangenis eindigt? En zo belanden we van een ouderwets spelletje Monopoly aan de rekentafel… Maar wees gerust, ik zal jullie het notitieblok en geslepen potlood besparen.

Monopoly en simulatie

Om te bekijken welk vakje op het spelbord het meest bezocht zal worden kunnen we een groot aantal potjes Monopoly simuleren waarbij we aan de hand van het gooien van de dobbelstenen één speler rond laten bewegen en vastgoed laten kopen. Door voor elk vakje bij te houden hoe vaak je hier bent geweest kunnen we bepalen welke vakjes op het spelbord de grootste bezoekkans hebben, rekening houdend met alle verborgen addertjes. Gezien de vele mogelijkheden om in de gevangenis te belanden is achter de tralies helaas de plek waar je jezelf gedurende een avondje Monopoly het meeste zult vinden.

Waar simulatie ook veelal leuke en zinvolle inzichten geeft, is in de dagelijkse praktijk. Waar winstkansen er wel degelijk toe doen. Denk aan: wat is de optimale lay-out van het magazijn zodat bottlenecks in productstromen kunnen worden voorkomen? Hoe kun je pallets het beste stapelen om ruimteverspilling tijdens transport te minimaliseren? Simulatie helpt je de beste strategie te bepalen door zo goed mogelijk de werkelijkheid na te bootsen. Dit geeft je de mogelijkheid om alle mogelijke scenario’s, alle mogelijke stapopties, alvast in kaart te brengen, zodat je aan de keukentafel niet meer hoeft te experimenteren maar gegarandeerd gaat winnen! Zo ook bij het optimaliseren en simuleren van grote vraagstukken: hoe meer inzicht (door simulatie), hoe beter je beslissing, product of dienst wordt. Zo zorg je ervoor dat een goed idee niet in de prullenbak (gevangenis) belandt, maar daadwerkelijk hoge ogen gooit voor je organisatie.

Monopoly en de dagelijkse praktijk

Zie je al welk straatje op het Monopoly bord je het beste kunt kopen? Een kleine hint: wanneer we onze kennis over bezoekkansen en dobbelstenen combineren dan weten we dat na een tijdje brommen gevangenen die hun cellen verlaten waarschijnlijk 6,7 of 8 stappen zetten. Weet jij welke vakken op het bord veel huur opleveren van de ex-criminelen en van jou binnen de kortste tijd een multimiljonair maken? Mocht je er niet uitkomen, neem dan contact met mij op, dan spelen we samen een spelletje Monopoly en nemen we jouw vraagstuk onder de loep.

Wil je daarnaast op de hoogte blijven van het laatste nieuws van CQM, volg ons op LinkedIn of meld je aan voor onze digitale nieuwsbrief. 

Hoofdfoto: Suzy Hazelwood op PxHere