Nog vijf maanden te leven

Hoe lang heb ik nog? Het is een vraag die onherroepelijk op tafel komt tijdens een slechtnieuwsgesprek waarin een patiënt te horen krijgt dat zij een ernstige ziekte heeft. De arts kan dan vaak een inschatting geven op basis van bijvoorbeeld ervaring. Maar ook statistiek speelt hier een belangrijke rol. Met behulp van overlevingsanalyse op data van eerdere patiënten worden schattingen steeds beter. Hoe moet je zo’n getal interpreteren? In deze post neem ik je mee in de totstandkoming van een sinister getal.

Gecensureerde data

De eerste stap om overlevingsduur te schatten is informatie verzamelen over patiënten. Een groep patiënten wordt bijvoorbeeld geobserveerd vanaf hun diagnose en hun gegevens, zoals de datum van de diagnose en de sterfdag, worden genoteerd. Het lijkt misschien makkelijk om met die diagnose- en sterfdata een gemiddelde levensduur vanaf diagnose te berekenen, maar in werkelijkheid is de analyse een stuk gecompliceerder. Namelijk, niet van elke patiënt wordt de sterfdag geobserveerd.

Stel bijvoorbeeld dat een aantal patiënten uit de groep verhuist naar een ander ziekenhuis, dan is niet bekend hoe het na de verhuizing met hen gaat. Het kan ook voorkomen dat een aantal patiënten zich nog goed voelt wanneer een studie wordt stopgezet. Dan blijft het de vraag hoelang zij nog leven na het stoppen van de studie. In beide gevallen blijft de exacte sterfdag onbekend en kan daardoor dus niet worden meegenomen in de berekening van de gemiddelde levensduur.

Deze patiënten simpelweg weglaten uit de berekening is zonde, want er is wel iets cruciaals bekend over de overleving van deze patiënten; zij leefden namelijk nog minimaal tot het moment dat ze verhuisden of de studie stopte. Dit is nuttige informatie, want het negeren van deze patiënten zou een onderschatting van de levensduur geven.

Dit soort data waarbij alleen minimale overleving bekend is in plaats van de exacte sterfdag noemen we gecensureerde data. Deze data bevatten nuttige informatie die belangrijk zijn om een goede schatting te maken, maar ze maken de statistische analyse wel een stuk lastiger. Simpelweg een gemiddelde nemen over de levensduur sinds diagnose kan niet meer.

Overlevingsanalyse

Voor een correcte analyse is een aparte tak binnen de statistiek ontstaan: de overlevingsanalyse. Deze techniek wordt vooral veel toegepast in de medische statistiek om de levensduur, of vrolijker, de tijd tot genezing, te berekenen. Maar in principe kan het gebruikt worden voor allerlei tijdsschattingen. Denk bijvoorbeeld aan de levensduur van een apparaat of batterij, hoelang het duurt voordat een klant zijn lidmaatschap opzegt, hoelang een klant aan de telefoon moet wachten op een klantenservicemedewerker, hoelang een busreis naar Parijs duurt, etc.

Door de gecensureerde data is het berekenen van een gemiddelde levensduur niet mogelijk. Daarom wordt in de overlevingsanalyse niet het gemiddelde berekend, maar de kans dat je nog leeft tot en met een bepaald tijdstip. Voor meerdere tijdstippen wordt bekeken hoeveel patiënten er nog onder observatie waren, en hoeveel van hen overleden sinds het vorige tijdstip. Op die manier worden de kansen geschat dat iemand bijvoorbeeld na twee weken, een maand, zes maanden en een jaar nog leeft.

Overlevingscurve

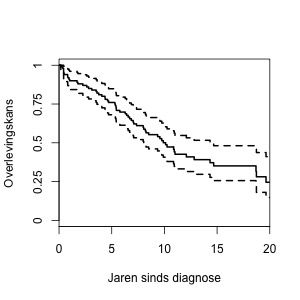
Deze schattingen worden weergegeven in een grafiek, de overlevingscurve. In Figuur 1 zie je een voorbeeld met verzonnen data. Op de horizontale as zie je de tijd sinds diagnose en op de verticale as staat de kans dat een patiënt dan nog leeft. We zien bijvoorbeeld dat de overlevingskans na vijf jaar ongeveer 0.75 is, ofwel 75 procent.

Een overlevingscurve begint altijd bij één, want op het moment van diagnose leven alle patiënten nog. Daarna daalt de grafiek, omdat er door de tijd heen helaas steeds meer patiënten overlijden.

De kansen worden berekend op basis van een steekproef, en daarom is er altijd wat onzekerheid in de schattingen. De twee stippellijnen in Figuur 1 geven die onzekerheid aan. De echte curve ligt waarschijnlijk tussen de twee stippellijnen, en hoogstwaarschijnlijk dicht bij de middelste lijn.

Mediane overleving

Patiënten krijgen niet altijd de volledige overlevingscurve te zien omdat die lastig te interpreteren zijn. Vaak wordt alleen de kans van één tijdstip gegeven, zoals de kans om na vijf jaar nog te leven.

Een andere optie is de mediane overleving. Dit is het moment waarop naar schatting de helft van de patiënten nog leeft. Ofwel, het moment waarop de overlijdenskans precies 50 procent is.

In Figuur 2 is de overlevingscurve uit Figuur 1 nog een keer weergegeven, nu met een horizontale lijn bij een kans van 0.5. Als je de lijn volgt tot deze de grafiek raakt, dan kun je op die plek de mediane overlevingsduur aflezen op de horizontale as, in dit voorbeeld ongeveer tien jaar. Dat betekent dat 50 procent van de patiënten na tien jaar nog in leven zijn.

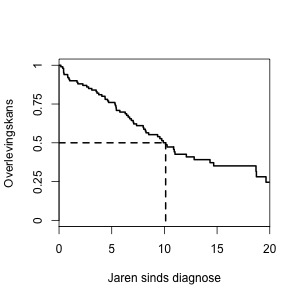
Het nadeel van het samenvatten van een hele curve in één enkel getal is natuurlijk dat je veel informatie verliest. Met een mediane overleving heb je wel een goede eerste indruk van de levensduur, maar je weet niets over het verloop van de kansen door de tijd heen. Je weet bijvoorbeeld van de eerste helft patiënten niet of zij vlak na diagnose al sterven of pas na een jaar of acht.

Je hoort wel eens “artsen zeiden: ‘u heeft waarschijnlijk nog maar drie maanden te leven,’ en kijk, na twee jaar leef ik nog steeds!”. Dat een voorspelling ernaast zit komt vaak door de grote verschillen tussen overleving van patiënten. In Figuur 2 zien we dat ook: de mediane overleving is tien jaar, maar 25 procent van de patiënten leeft zelfs nog na twintig jaar.

Soms wordt een overlevingskans na verloop van tijd aangepast. Als een patiënt zich bijvoorbeeld bovengemiddeld lang goed voelt, dan is dit reden om de verwachte overleving naar boven bij te stellen.  

Gepersonaliseerde kansen

Bij de tot nu toe getoonde overlevingscurves is de data van alle patiënten op een hoop gegooid. Maar je kunt je voorstellen dat er veel factoren zijn die de overlevingskansen beïnvloeden waardoor deze uiteenlopen, bijvoorbeeld de levensstijl van een patiënt of bepaalde fysieke eigenschappen. Als patiënt wil je natuurlijk graag dat daar rekening mee wordt gehouden bij de schatting; je hebt immers het meest aan een gepersonaliseerde overlevingscurve die helemaal op jou is afgestemd.

Een simpele manier om verschillen tussen patiënten mee te nemen is om een aparte curve te maken per subgroep patiënten. Je kunt bijvoorbeeld een splitsing maken tussen patiënten die wel en niet roken en voor beide groepen een overlevingscurve maken, zoals in Figuur 3. Op deze manier kun je de groepen makkelijk vergelijken. We zien in Figuur 3 bijvoorbeeld dat de niet-rokers veel hogere overlevingskansen hebben, en dus ook een hogere mediane overleving.

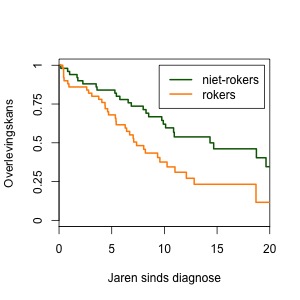
Het vergelijken van groepen op deze manier kan alleen als je maar een paar factoren tegelijk bekijkt. Stel dat bijvoorbeeld ook gezonde en ongezonde eetgewoontes worden meegenomen. Je krijgt dan vier curves om te vergelijken: voor niet-rokers met gezonde eetgewoontes, voor niet-rokers met ongezonde eetgewoontes, en dezelfde splitsing voor de rokers. Hoe meer groepen, hoe lastiger om alle curves te vergelijken.

Voor veel factoren, en ook voor continue data zoals leeftijd, bedachten statistici andere oplossingen. De extra informatie wordt meegenomen in een model dat alles tegelijk vergelijkt. Uit het model wordt per persoon een overlevingscurve gemaakt, gebaseerd op gegevens van eerdere patiënten die het meest op die persoon lijken.

Het blijven schattingen

Helaas kunnen de modellen nooit een perfecte schatting geven. Dat is altijd afhankelijk van de data die beschikbaar is; in hoeverre lijken eerdere patiënten op een nieuwe patiënt en zijn er genoeg om een betrouwbare schatting te maken? Bovendien is het nog de vraag of alle factoren die invloed hebben op overleving wel in het model zijn opgenomen. Is er niks belangrijks over het hoofd gezien?

Al met al geven overlevingsanalyses goede indicaties van de tijd die een patiënt nog rest. Niet meer dan dat. Het blijven schattingen. Op de vraag ‘hoe lang heb ik nog?’ volgt dan ook een minder precies antwoord dan het tijdens het slechtnieuwsgesprek misschien lijkt.

Credit

Hoofdfoto: JESHOOTS op Unsplash

Grafieken: Sanne Willems