Onzekerheid zichtbaar maken

Onlangs was ik op een lezingenmiddag waar we het hadden over het communiceren over onzekerheid in data. De discussie ging erover hoe dat door verschillende onderzoekers wordt gedaan en of dat wel overkomt bij de lezers. De meest gebruikte manier zijn van die ‘pootjes’ op grafieken: foutbalken of error bars.  Hieronder zie je zo’n grafiek met foutbalk. Het is een fictief voorbeeld, geïnspireerd door een rapport over basisonderwijs. Het gaat over de scores op een standaardleestoets op de basisscholen. Rechts heb ik de bovenkant van de grafiek een beetje uitvergroot, zodat de waarden wat beter af te lezen zijn.

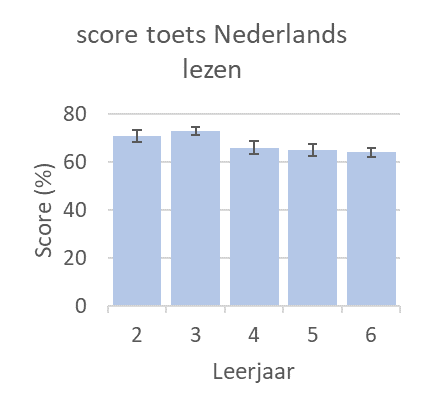
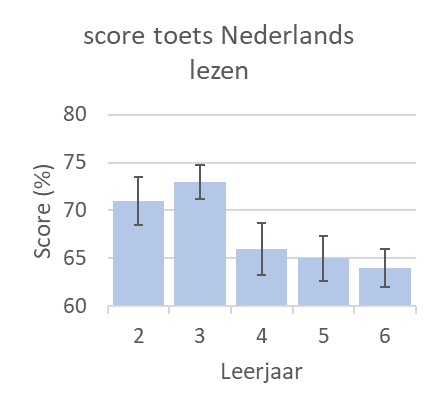
1 (fictief voorbeeld) Gemiddeld score per leerjaar op leestoets in 2020. Foutbalk toont 95%-betrouwbaarheidsinterval. n=35 scholen. Rechts, zelfde grafiek uitvergroot.

Foutbalk: de onzekerheid rond het gemiddelde

Laten we ons concentreren op leerjaar 2. Gemiddeld was de score 71 procent en de pootjes, officieel dus foutbalk of error bar, lopen van 68,5 procent tot 73,5 procent. Ik zou het niet vreemd vinden als lezers dan denken: de gemiddelde score was 71 procent, en dat varieerde van sommige scholen met 68,5 procent tot sommige scholen met 73,5 procent score. De scholen zitten dus allemaal mooi dicht bij elkaar. Maar dat is niet wat de foutbalk wil vertellen. Wat dan wel?

De foutbalk vertelt dat de auteurs van deze grafiek niet helemaal zeker zijn over dat gemiddelde. Ze hebben namelijk niet alle scholen van Nederland onderzocht. Volgens het onderschrift onderzochten deze onderzoekers maar 35 scholen, van de meer dan 6000 die we in Nederland hebben. En gemiddeld op die 35 scholen was de score 71 procent. Maar als ze 35 andere willekeurige scholen hadden gebeld, dan was het gemiddelde waarschijnlijk net iets anders geweest.

Betrouwbaarheidsinterval

Onderzoekers kunnen verschillende manieren kiezen om de foutbalk te berekenen. In de tekst onder de figuur is te lezen dat ze hier met de foutbalk het 95%-betrouwbaarheidsinterval weergeven. Dit betrouwbaarheidsinterval is het gemakkelijkst te interpreteren en hopelijk in de meeste vakgebieden het meest gebruikt.

Dit betrouwbaarheidsinterval betekent, dat op grond van de gegevens die ze hebben verzameld, de auteurs schatten dat als ze alle basisscholen van Nederland hadden gebeld (meer dan 6000 dus), de gemiddelde score hoogstwaarschijnlijk ergens tussen 68,5 procent en 73,5 procent was uitgekomen. Het zou een beetje mee kunnen vallen, dat het gemiddelde over alle >6000 scholen misschien wel 73,5 procent is, of wat kunnen tegenvallen dat het maar 68,5 procent is, maar waarschijnlijk iets daartussenin. Hadden ze meer scholen gebeld dan die 35, dan waren de auteurs waarschijnlijk zekerder geweest over hun schatting van het gemiddelde, en dan hadden we kortere foutbalkjes gezien.

Standaardfout

Sommige auteurs geven met de foutbalk niet het 95%-betrouwbaarheidsinterval weer, maar de zogeheten standaardfout. Een maat die ruwweg de helft van het betrouwbaarheidsinterval beslaat. Als het goed is, staat dat dan in de tekst onder de grafiek. De lezer moet dan in zijn hoofd de lengte van de foutbalk verdubbelen om de interpretatie hierboven te krijgen.

Zo’n foutbalk toont dus niet de variatie tussen de scholen, maar hoe zeker de auteurs ervan zijn dat ze het gemiddelde goed hebben geschat.

Variatie tussen de scholen

Maar hoe zit het dan met de verschillen tussen de scholen? Dat kunnen we niet eenvoudig uit deze grafiek opmaken. Dat hangt er namelijk ook van af hoe die schoolresultaten verdeeld zijn. Zijn ze een beetje symmetrisch verdeeld rondom dat gemiddelde van 71 procent of juist wat scheef met vrij veel ietsje hogere resultaten en een paar heel veel slechtere. In ieder geval zal die spreiding groter zijn dan wat dit foutbalkje aangeeft.

Als de schoolresultaten een mooie symmetrische verdeling (normale verdeling) vertonen, dan zou de spreiding van die 35 onderzochte scholen ongeveer kunnen zijn zoals de losse stipjes in het plaatje hieronder: elk stipje een gemiddelde score voor een school. Dus een uitschieter omhoog naar een school met een score van 83 procent kan er best een keer bij zitten, maar een uitschieter omlaag naar 53 procent ook. Onder alle >6000 scholen kunnen misschien nog wel een paar extremere uitkomsten zitten. En de scores van de individuele kinderen, die variëren natuurlijk nog meer.

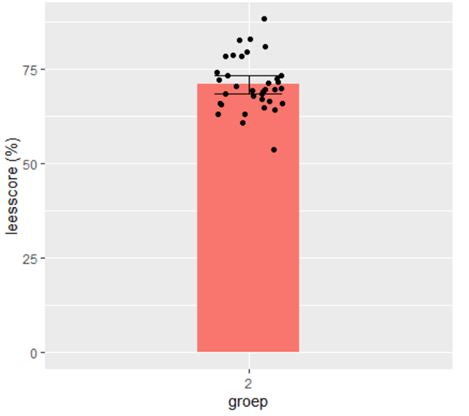
2 (fictief voorbeeld) Gemiddeld score op leestoets in 2020 in leerjaar 2. Foutbalk toont 95procent betrouwbaarheidsinterval. n=35 scholen. Stippen tonen gemiddelde score op individuele scholen in de steekproef.

De variatie in de waarnemingen is dus groter dan de onzekerheid over het gemiddelde.

Helaas is in sommige rapporten de tekst onder de grafiek niet zo uitgebreid. Of de foutbalk voor het 95%- betrouwbaarheidsinterval staat of voor de standaardfout, staat er soms niet bij. En op hoeveel scholen of andere waarnemingen het gemiddelde is gebaseerd is ook niet altijd gemakkelijk terug te vinden. Tja, die communicatie, die zou nog best wat beter kunnen.

Verder lezen

Blog Kurt Verstegen over betrouwbaarheidsinterval
Wikipedia over de foutbalk (Engelstalig)
Wikipedia over de standaardfout (Engelstalig)