Zwangerschap voorspellen (­2)

Na een jaar proberen zijn jullie helaas niet zwanger. De arts zegt dat je het nog wel zes maanden langer kunt proberen voordat behandeling nodig is. Zes maanden later zitten jullie weer tegenover de arts zonder zwangerschap. Wat nu?

Ken je het koppel uit het rekenvoorbeeld in mijn vorige post nog? Ze werden door de arts naar huis gestuurd omdat hun kans op natuurlijke zwangerschap best groot was, 37 procent. Deze was dus boven het afkappunt van 30 procent. Ze spraken af het zes maanden langer te proberen in plaats van door te gaan met inseminatie of ivf. In deze post gaan we verder met dat verhaal. (Tekst gaat verder onder het tekstblok)

Wat ik hier eerder over schreef
Het komt vaker voor dan je denkt . Een koppel wil graag zwanger worden maar het lukt helaas niet. Na een jaar proberen, stuurt de huisarts hen door naar de specialist voor tests. Vaak kan die geen duidelijke reden vinden voor het uitblijven van een zwangerschap, wat we onverklaard subfertiel noemen (zie ook deze  post). Een deel van deze koppels kunnen nog zwanger worden op natuurlijke wijze, dus het dilemma is: gaan we behandelen of niet? Is het eigenlijk wel nodig? In deze post schreef ik dat voorspelmodellen kunnen helpen bij het kiezen van een behandeling, of het nou inseminatie of ivf (fertilisatie in het lab) is. Het ene koppel is immers de andere niet: sommige zijn jonger of al eerder zwanger geweest, waardoor hun kans op zwangerschap misschien wat hoger is dan die van oudere koppels. Het is dan een goede optie om af te wachten en langer te proberen om natuurlijk zwanger te worden aangezien behandelingen stressvol, invasief en duur zijn. Maar wat als je kiest voor afwachten en het nog steeds niet lukt? Je zit dan later met precies hetzelfde probleem. Wat dan?

Kiezen met voorspelmodellen
In mijn vorige post schreef ik dat voorspelmodellen handig zijn om de patiënt te informeren en in overleg met de arts te beslissen over de fertiliteitsbehandeling. Ter illustratie weer het voorbeeld uit die post: stel je een onverklaard subfertiel koppel voor waarvan de vrouw 35 jaar oud is, die het anderhalf jaar lang hebben geprobeerd, al eerder zwanger zijn geweest en er 30 procent beweeglijk zaad uit het onderzoek kwam. Dit koppel heeft 37 procent kans op een doorgaande zwangerschap in het jaar na diagnose, terwijl het bij ivf 62 procent is.
(Wil je zelf meerekenen? Doe dit dan hier voor specifiek natuurlijke zwangerschap of hier voor alle drie de opties. Lees dan wel ook de vorige post hierover voor de haken en ogen.)

Stel: zes maanden later is het koppel helaas nog niet zwanger. Na een telefoontje hebben ze een nieuwe afspraak en voor ze het weten, zitten ze weer tegenover dezelfde arts. Terug bij af…

Aan de ene kant lijkt er niets veranderd: er zijn nog steeds drie opties. Met de arts overleggen ze weer wat de verstandigste keuze is. Aan de andere kant hebben ze het zes maanden langer geprobeerd. Misschien dat ze optimistisch blijven en het toch langer willen proberen. Misschien dat behandeling ze bij nader inzien niets lijkt. Of… misschien is hun geduld op, gaat het ten koste van hun relatie en verliezen ze de hoop.

Het uitstellen van behandeling kan leiden tot een terugkeer van het probleem. Met één beslissing ben je er dus nog niet. Het échte dilemma voor koppels met onverklaarde subfertiliteit is niet ­of ze behandeling moeten krijgen, maar wanneer.

Wat kunnen wij als onderzoekers  doen om daarbij te helpen? Eerst terug naar de voorspelmodellen. Wat als we deze opnieuw invullen met de nieuwe informatie?

Waar het voorspelmodel fout zit

Stel nu dat we het voorspelmodel voor natuurlijke zwangerschapskans opnieuw invullen, maar nu met een half jaar erbij: de vrouw is dus 35.5 jaar en ze hebben het twee jaar geprobeerd. De geüpdatete kans is 34 procent, een daling van slechts 3 procent ten opzichte van zes maanden geleden. Het is lastig te verklaren, maar het ‘voelt’ onrealistisch. Alsof er niets gebeurd is. Waren die zes maanden betekenisloos? Ook blijft de beslissing volgens de richtlijn hetzelfde, de kans is namelijk nog steeds boven de 30 procent.

Hoe kan dit?

Het probleem is dat we het voorspelmodel helemaal niet kunnen toepassen in deze situatie. Het is bedoeld voor de groep koppels die zojuist horen dat hun diagnose onverklaarde subfertiliteit is. We passen het nu toe op de groep koppels die een half jaar na die diagnose nog niet zwanger zijn. Klinkt het misschien alsof dat niet veel uitmaakt, alsof het dezelfde groep is? Onderstaand rekenvoorbeeld laat zien dat het er wel toe doet.

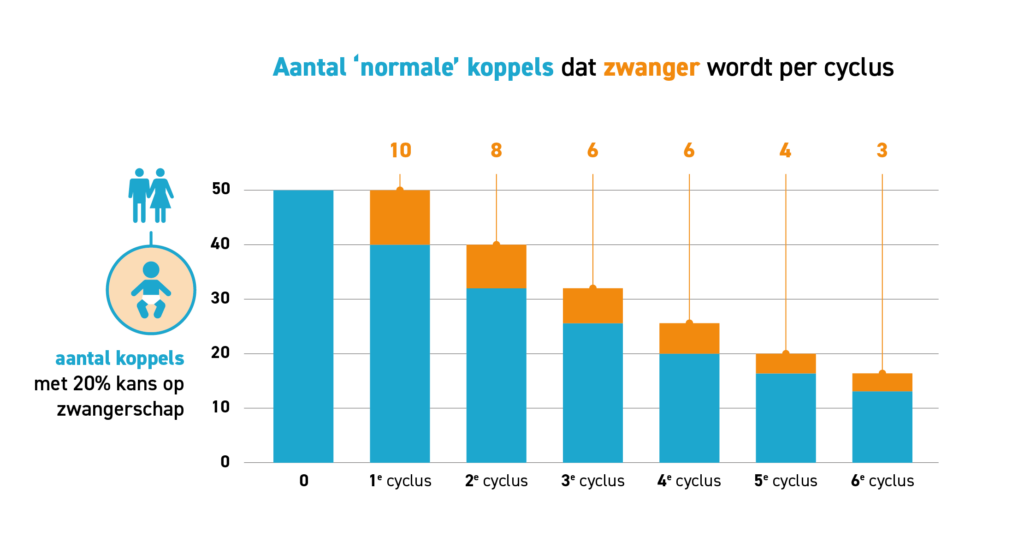
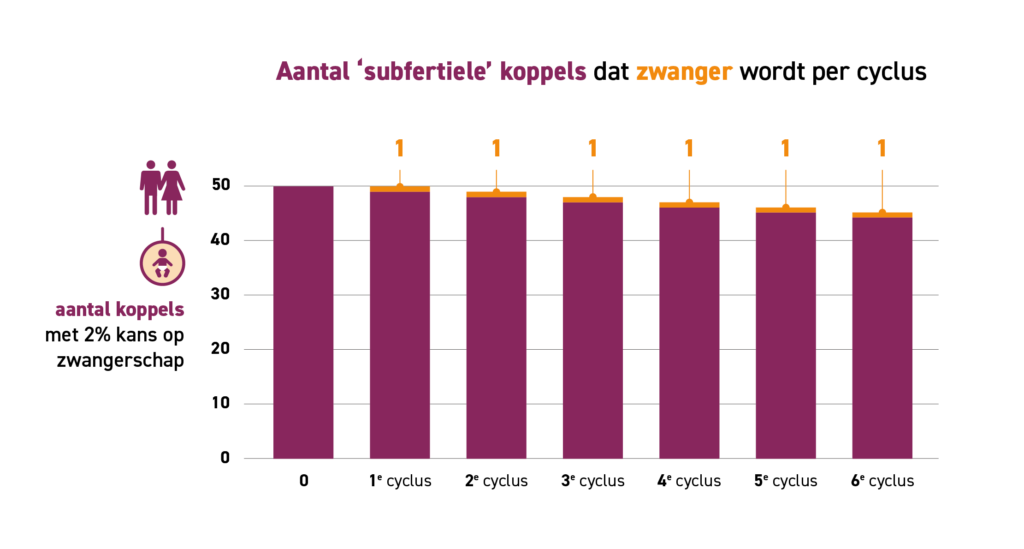
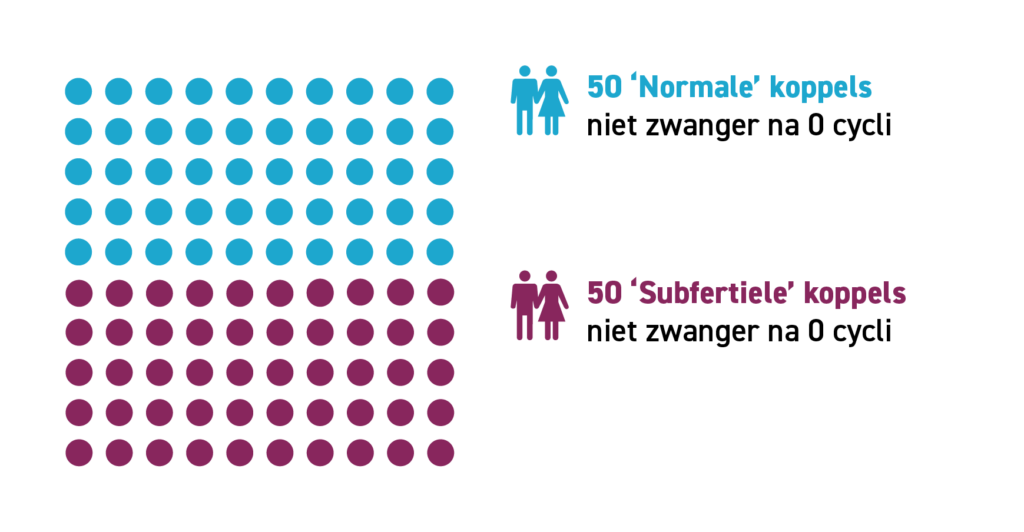
Laten we doen alsof we precies de zwangerschapskans van alle koppels weten, wat in de praktijk natuurlijk niet zo is. Stel dat de gehele groep koppels die met hun kersverse diagnose tegenover de arts zit, bestaat uit de helft ‘normale’ koppels met een zwangerschapskans van 20 procent per cyclus en voor de helft ‘subfertiele’ koppels met een kans van 2 procent per cyclus. Stel dat dit er 50 per groep zijn, 100 in totaal. De gemiddelde kans per cyclus is dan (0.2 + 0.02) / 2 * 100 = 11 procent. Net als de berekening in deze post verwachten we dat na zes cycli er ongeveer 43 van de 100 zwanger zijn geworden, waarvan 37 ‘normale’ en 6 ‘subfertiele’. Zie voor een visuele weergave van de zwangerschappen per groep per cyclus Figuur 1A.

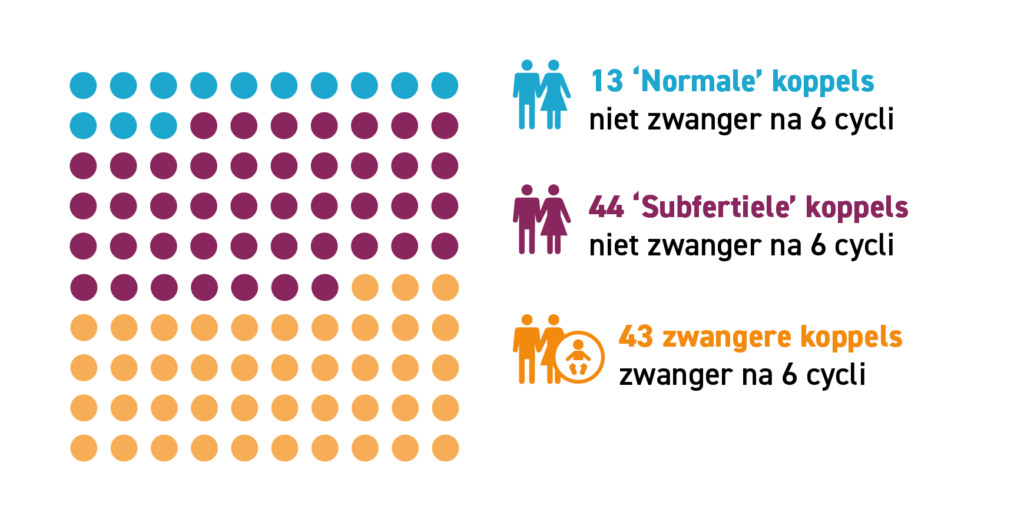
Als we opnieuw de gemiddelde kans berekenen in de overgebleven 57 koppels, dan is deze nu ((13*0.2) + (44*0.02)) / 57 * 100 = 6 procent. Deze kans is bijna gehalveerd! De ‘selectie’ die heeft plaatsgevonden na zes cycli is in dit voorbeeld groot. In Figuur 1B zie je het verschil in de samenstelling tussen de groepen: eerst bij diagnose en daarna zes cycli later. De groep na zes maanden selectie valt niet goed te vergelijken met de groep waarmee we begonnen: er zijn nu relatief meer subfertielen.

Dat maakt dit een moeilijk methodologisch en statistisch probleem: de groep koppels die we onderzoeken, verandert continu. Maar: we weten dus dat de kans daalt naarmate er meer selectie plaatsvindt! Andersom kan eigenlijk niet. Dat is de sleutel voor de oplossing.

Herhaald voorspellen: ‘dynamisch’

We weten dus ongeveer hoe die selectie en daling eruit ziet: we beginnen met een bepaalde patiëntengroep, maar deze wordt steeds ‘slechter’ in termen van de gemiddelde kans. We kiezen daarom een ‘dynamisch’ statistisch model dat dat kan vatten om het in ons voordeel te gebruiken. We hebben er niets aan om dat te doen met bedachte voorbeelden, dus laten we de stap zetten naar echte koppels en echte data. We pasten het model toe in een onderzoek met hetzelfde Nederlandse cohort van ongeveer 5,000 koppels waar destijds het ‘Hunault’ model voor natuurlijke zwangerschap op was gebaseerd (zie ook de vorige post).

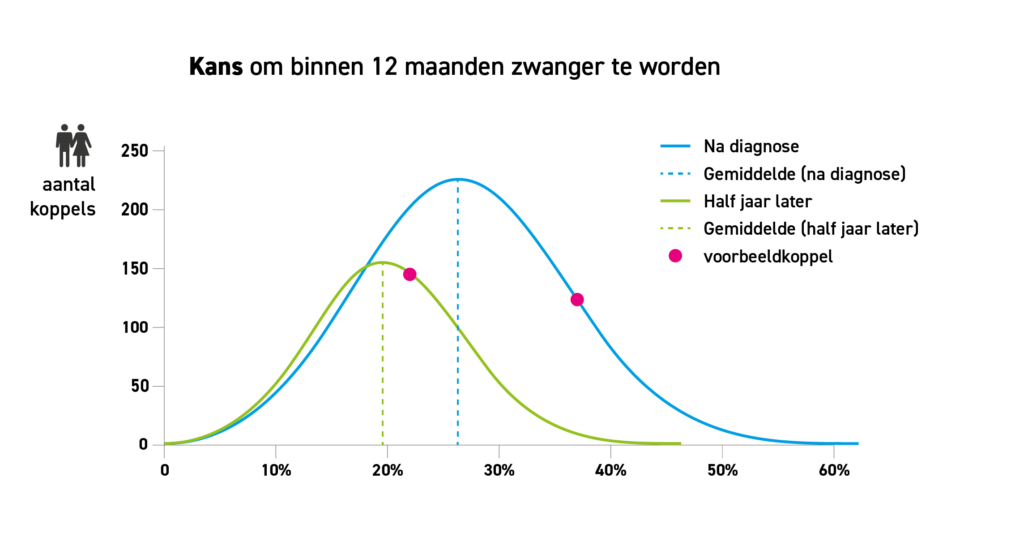
Nadat we het dynamische model op dit cohort hebben gedraaid, kunnen we meer! In Figuur 2 zie je in het lichtblauw de verdeling van kansen voor alle koppels om binnen het jaar na diagnose van de gehele groep zwanger te worden, varierend van ~1 procent tot bijna 60 procent. De hoogte geeft het aantal koppels weer die in dit onderzoek ongeveer dezelfde kansen hadden. In de Figuur zie je in het groen de verdeling van zwangerschapskansen voor koppels die na een halfjaar nog niet zwanger waren, geüpdate voor het jaar dat op dat moment start. Zie je het verschil? Zoals in het rekenvoorbeeld van eerder, is het een figuur die eigenlijk steeds meer naar links schuift, richting de nul. We zijn er immers vrijwel zeker van dat koppels die hun hele vruchtbare leven lang proberen en dan nog steeds niet zwanger zijn, een kans hebben die vrijwel nul is.

Toepassen op het eerdere koppel

We pasten dit model toe op een cohort van onverklaard subfertiele koppels in Schotland, waar het goed bleek te werken. Nu hebben we voldoende vertrouwen in het model om het te kunnen gebruiken in de praktijk, bijvoorbeeld om het koppel waarmee ik deze post begon te adviseren! Hun kans op zwangerschap was 37 procent in het jaar na diagnose. We vinden met het dynamische model dat na zes maanden selectie de kans over het volgende jaar ‘slechts’ 22 procent is (zie ook de roze stippen in Figuur 3). De daling van 15 procent ten opzichte van een halfjaar eerder lijkt een stuk realistischer dan de 3 procent daling die uit het oude model rolde. Ook is het voor de richtlijn nu een stuk duidelijker dat ze wél beter af lijken te zijn met behandeling, nu deze kans ruim onder de 30 procent is. Zo is het dus een stuk makkelijker om de knoop door te hakken.

Conclusie

Via een ingewikkeld methodologisch zijstapje hebben we dus een mooie oplossing gevonden voor dit lastige klinische probleem. Met behulp van het ‘dynamische’ model kunnen we op ieder gewenst moment na diagnose voorspellen, wat accurater is en realistischer lijkt. Dit levert nuttige informatie op om in het overleg met de arts te gebruiken.

Hopelijk wordt het model uiteindelijk opgenomen in de nieuwe nationale richtlijn voor onverklaarde subfertiliteit. Het is echter lastig om het te combineren met het ‘Hunault’ model wat op het moment al in de klinische praktijk gebruikt wordt.

Zie voor meer informatie en een printbare versie van het model wat met een pen in te vullen valt, een zogenaamde nomogram, de publicatie, vrij toegankelijk. Ook de volledig uitgewerkte formule staat daar in het online supplementair materiaal.

Heb je nog vragen over deze modellen en/of posts? Benader me gerust met je vragen via r.vaneekelen@amsterdamumc.nl, LinkedIn of Twitter via @RikEekelen.

Bronnen:

• Freya website (Hunault calculator)
• YourFertility.org.au website (calculator voor de drie opties)
• Dynamisch voorspelmodel
• Validatie van het dynamische voorspelmodel

Infographics gemaakt door Elke Uijtewaal (Instagram)

Verder lezen

Voor meer informatie en een luisterend oor kun je terecht bij de patiëntenvereniging Freya voor mensen met vruchtbaarheidsproblemen:

www.freya.nl