Waarschijnlijk baseer jij veel beslissingen op statistisch geschatte kansen. Als komend weekend de kans op mooi weer groot is, besluit je misschien wel om naar het strand te gaan. Wanneer je een vakantie boekt, doe je er wellicht een annuleringsverzekering bij. En de keuze voor of tegen vaccinatie kan ook te maken hebben met wat jij onder een kleine kans op bijwerkingen verstaat.
Waarschijnlijk, wellicht, misschien, grote kans. Dit zijn allemaal manieren om een kans in woorden uit te drukken. Ook professionals doen dat, vooral in gesprekken. Je arts vertelt bijvoorbeeld dat je een grote kans hebt op genezing, maar dat mensen zoals jij vaak last hebben van bijwerkingen van het medicijn.
Maar wat bedoelt je arts precies met “grote kans” en “vaak”? Welke kans heeft hij in gedachten? En vooral: komt deze kans overeen met hoe jij hem interpreteert? Zou een andere arts dezelfde woorden kiezen voor die kansen? Om inzicht te krijgen in de verschillen onderzocht ik samen met mijn collega’s Ionica Smeets en Casper Albers de variatie in de interpretatie van kans- en frequentiewoorden.
Waarom in woorden?
De toekomst is onzeker. Als we toch voorspellingen maken, bijvoorbeeld over de kans op regen, dan doen we dat met statistische modellen. Deze modellen gebruiken gegevens uit het verleden, maar die bieden natuurlijk geen garantie voor de toekomst. Een voorspelling blijft altijd een schatting en die is nooit exact.
Deze onzekerheid is een reden om terughoudend te zijn in het geven van exacte getallen. Dat zou namelijk de verwachting kunnen scheppen dat de kans precies bekend is, in plaats van geschat. Vooral in gesprekken gebruiken we daarom vaak kanswoorden (onwaarschijnlijk, grote kans, misschien) of frequentiewoorden (vaak, nooit, meestal). Deze uitspraken geven indirect al de statistische onzekerheid aan.
Maar juist door die indirecte onzekerheid kan er verwarring ontstaan. Want wat als je arts met grote kans 90 procent kans op genezing bedoelt, en jij denkt dat de kans “maar” 60 procent is? Zo’n verschil in interpretatie kan ervoor zorgen dat jij sterk twijfelt over een behandeling die eigenlijk een erg grote kans van slagen heeft.
Grote variatie in interpretatie
Stel je leest de zin “Waarschijnlijk wint het team de wedstrijd.”, hoe groot denk jij dat dan de kans is dat het team de wedstrijd wint? In ons onderzoek legden wij dat soort vragen voor aan onze deelnemers, elke zin met een ander kans- of frequentiewoord.
In Figuur 1 zie je de resultaten voor waarschijnlijk. Op de horizontale as staan alle percentages van 0 tot 100 procent en de hoogte van de grafiek geeft aan hoeveel deelnemers een bepaald percentage kozen. Voorbeeld: de grafiek is het hoogst bij 80 procent, dit betekent dat dat het meest gekozen percentage is voor de interpretatie van waarschijnlijk.
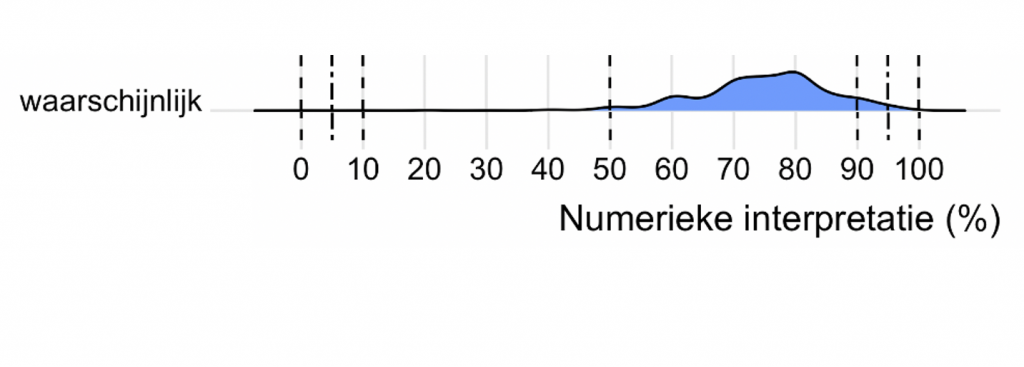
De grafiek is erg breed. Hij begint bij ongeveer 45 procent en heeft een lange staart die doorloopt tot 100 procent. De interpretatie van het woord waarschijnlijk is dus erg gevarieerd.
Tussen 60 procent en 90 procent is de grafiek vrij hoog. Dus als jij waarschijnlijk gebruikt om een kans van 90 procent aan te duiden, is het niet ondenkbaar dat iemand anders dit interpreteert als een kans van nog geen 70 procent. Dat kan dus veel verwarring opleveren.
Figuur 2 geeft de resultaten van alle onderzochte kans- en frequentiewoorden weer. Bij de meeste uitspraken zie je hetzelfde verschijnsel: de grafieken zijn heel breed. Er zitten dus grote verschillen in de interpretatie van veel van deze woorden.
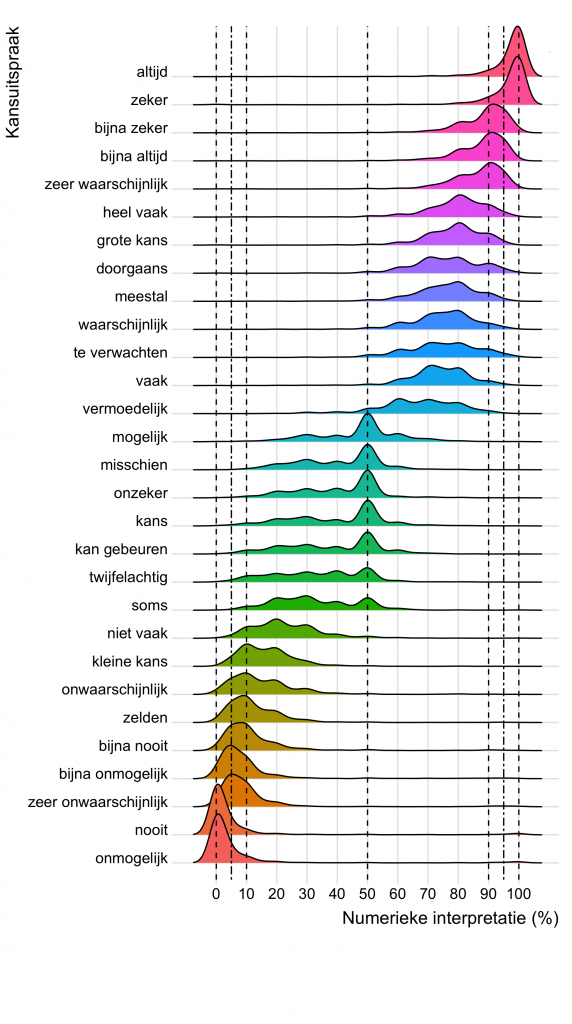
Alleen bij de extreme uitspraken, zoals altijd, zeker, nooit en onmogelijk, heeft iedereen bijna dezelfde interpretatie. De grafieken zijn minder breed en er zijn hoge pieken rond 100 en 0 procent. Dit is niet onverwacht; bij deze woorden is er weinig ruimte voor eigen interpretatie. Wat me wel verbaast is dat sommige deelnemers een onmogelijke gebeurtenis toch nog een kans van 10 procent gaven. Het onmogelijke is dus toch mogelijk?
Helpt ervaring?
Hoe zit dat bij de experts? Je zou misschien verwachten dat statistici het onderling wel eens zijn over de interpretatie van verbale kansuitspraken. Daarom vroegen wij deelnemers of zij regelmatig (wekelijks of maandelijks) statistische analyses doen. Zo konden we de antwoorden van de twee groepen vergelijken en nagaan of ervaring met statistiek voor overeenstemming in de interpretatie zorgt.
In Figuur 3 vergelijken we de resultaten van de twee groepen voor vijf kansuitspraken. De rode grafieken geven de antwoorden van de statistici weer, en die van de andere deelnemers zijn blauw. De paarse gebieden laten de overlap tussen de twee groepen zien.
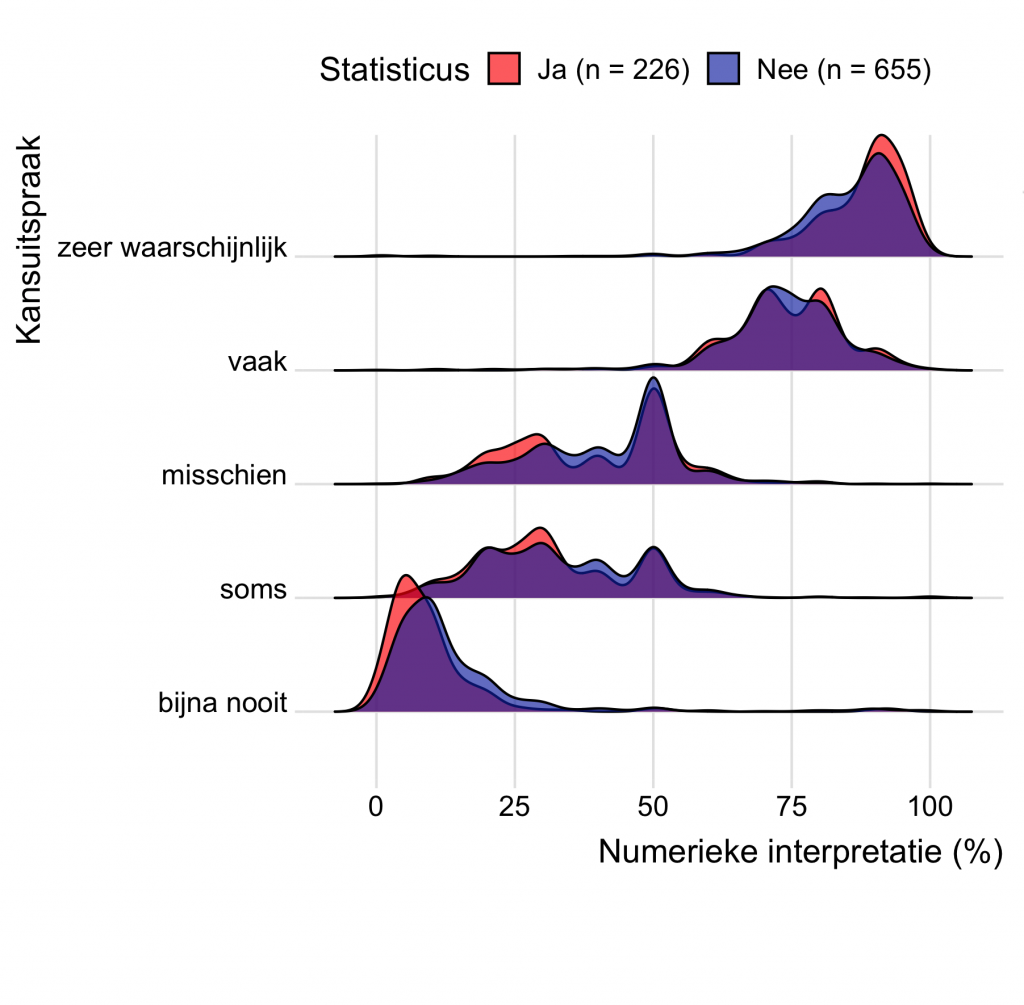
Er is veel overlap tussen de twee groepen, het grootste gedeelte van de grafiek is namelijk paars. En statistici zijn het onderling ook niet eens over de interpretatie van de verschillende uitspraken, want ook de rode grafieken zijn erg breed.
Meer ervaring met kansen zorgt dus niet voor een eenduidige interpretatie. Misschien is dit niet zo vreemd. Als ik met mijn collega’s de uitkomsten van modellen bespreek, dan doen we dat eigenlijk altijd in getallen. We gebruiken onderling dus zelden kanswoorden en bespreken daarom ook nooit de interpretatie daarvan.
Hoe dan wel?
Niet iedereen interpreteert kanswoorden op dezelfde manier. Dit kan tot verwarring leiden. Hoe lossen we dat op? Een voor de hand liggende oplossing lijkt om de verbale kansuitspraken te verbannen en alleen nog met numerieke percentages te werken. Maar helaas is het niet zo makkelijk. Veel mensen vinden percentages namelijk lastig te begrijpen. Het gebruik van percentages leidt dus óók tot misverstanden.
Wetenschappers aan verschillende universiteiten doen onderzoek naar de duidelijkste weergave van kansen. Zo bekijken ze de combinatie van woorden en kansen en het effect van verschillende weergaven van percentages, bijvoorbeeld “25 procent” versus “25 van de 100”. Ook onderzoeken ze welke factoren van invloed zijn, zoals gecijferdheid.
Dé oplossing is nog niet gevonden. Het is wel duidelijk dat woorden alleen niet genoeg zijn. Gebruikt jouw arts toch een keer een kanswoord? Vraag dan om verduidelijking.
Verantwoording
Deze post is gebaseerd op de resultaten van een onderzoek dat de auteur heeft uitgevoerd in samenwerking met Prof.dr. Ionica Smeets en Prof.dr. Casper Albers. De volledige resultaten zijn gepubliceerd in het wetenschappelijke artikel Willems S., Albers C. & Smeets I. (2020), Variability in the interpretation of probability phrases used in Dutch news articles — a risk for miscommunication, JCOM: Journal of Science Communication 19(02): A03.
Hoofdfoto: Dice games, Joy Shrader op PublicDomainPictures.net













Dank Sanne voor dit interessante en relevante onderzoek dat inderdaad de statistiek dichter bij de mensen brengt.
Ga door op de ingeslagen weg!
Met vriendelijke groet,
Jos Berkemeijer
2,5% ipv 25%?
Bedankt voor het doorgeven, is aangepast!
Interessant stuk! Maar ik erger mij eraan hoe in de grafiek er nog oppervlakte bestaat voor 0% en na 100%, wat impliceert dat er mensen zijn die denken dat “onmogelijk” een kans van -10% aangeeft, evenzo dat “altijd” een kans van 110% impliceert.
Ja dat blijft jammer, maar er is bewust gekozen voor deze grafieken omdat ze de data toch het meest inzichtelijk maken van de opties die we geprobeerd hebben. Er staan voorbeelden van histogrammen op p.14 van http://casperalbers.nl/files/oratie.pdf, maar het probleem met histogrammen is je dan vooral de pieken ziet bij ronde getallen; mensen zijn geneigd om bijvoorbeeld voor 90% te kiezen ipv 89% of 91%.
Is uit de data ook te halen hoe, naast de subcategorie van statistisch onderlegde, de subcategorie van artsen hierop antwoordt?
Uit deze data niet; we hebben deelnemers alleen gevraagd of ze regelmatig statistische modellen maken, niet of ze arts zijn. Er zijn wel onderzoeken gedaan onder artsen, zie bijvoorbeeld
het artikel “How Medical Professionals Evaluate Expressions of Probability” van Kong et al. uit 1986.
Interessant en erg overzichtelijk weergegeven! Mijn complimenten en dank! Ik ga figuur 2 uitprinten en boven mijn bureau hangen.
En ik ben eigenlijk direct nieuwsgierig naar een onderzoek dat hierop kan aansluiten. Namelijk, soms wil een schrijver in een tekst aangeven dat iets ‘goed’ is, ‘sterk’, ‘significant beter dan verwacht’, of ‘niet goed’. Maar hoe goed is ‘goed’? Hoe significant is ‘significant’? En wordt ‘niet goed’ hetzelfde geïnterpreteerd als ‘slecht’? Natuurlijk kan je overal wiskundige termen, percentages en andere getallen aan koppelen, maar zoals je zelf ook al aangeeft wil je ook dat een tekst begrijpelijk leesbaar kan zijn voor een brede doelgroep. Dan is het erg handig om te weten hoe dergelijke termen in Nederland geïnterpreteerd worden. Hopelijk vind je deze suggestie zinvol en geeft het je inspiratie om mee aan de slag te gaan!
Bedankt voor de suggestie, dat is zeker ook interessant om naar te kijken. Er zijn zo veel leuke onderzoeken te doen, maar helaas zo weinig tijd 😉
Dankjewel Sanne- waardevol onderzoek. Toont de relativiteit van woorden om een eigen idee over te brengen. Goed bezig! Bavo
Leuk onderzoek, maar ik zie dat de respondenten niet echt NL representatief zijn.
Zouden de uitkomsten heel erg anders zijn als jullie meer doorsnee NL hadden ondervraagd?
Klopt, deelnemers zijn gevonden via Twitter en dat geeft geen representatieve steekproef voor NL. Maar zelfs binnen deze homogene groep zien we flinke verschillen interpretatie. Ofwel, zelfs mensen die redelijk op elkaar lijken zijn het niet eens over de interpretatie, dat zagen we ook onder de statistici. Ons vermoeden is daarom dat er vergelijkbare, of zelfs nog meer, variatie zal zijn als het wel een representatieve steekproef was met nog meer verschillen tussen deelnemers.
Discussie met mijn dochter bracht de volgende gedachte: context doet ertoe bij het interpreteren van worden als vaak, zelden, … Als 5% van de mensen die gaan fietsen in Amsterdam sterven dan vindt ik dat vaak. Als 5% van de mensen die een vliegreis boeken een uur vertraging heeft dan vindt ik dat zelden.
Context heeft zeker invloed, dat maakt het ook onmogelijk om één interpretatie te geven per woord die in elke context klopt. In ons onderzoek hebben we geprobeerd om de context neutraal te houden om de invloed daarvan te verminderen. Er zijn ook onderzoeken waarin gericht wordt op één bepaalde context, maar zelfs dan is er geen eenduidige interpretatie van alle kanswoorden.
In aansluiting hierop het volgende, uit de wereld van de bijsluiters bij geneesmiddelen: de verplichte aanduiding van de frequentie waarmee bijwerkingen kunnen voorkomen.
Zeer vaak: komt voor bij meer dan 1 op de 10 gebruikers.
Vaak: komt voor bij minder dan 1 op de 10 gebruikers.
Soms: komt voor bij minder dan 1 op de 100 gebruikers.
Zelden: komt voor bij minder dan 1 op de 1000 gebruikers.
Zeer zelden: komt voor bij minder dan 1 op de 10.000 gebruikers.
Klopt! Maar zelfs met deze tabel worden de kansen niet altijd juist ingeschat, zie bijvoorbeeld Knapp, P., Gardner, P. H., & Woolf, E. (2015). Combined verbal and numerical expressions increase perceived risk of medicine side-effects: a randomized controlled trial of EMA recommendations.
Maar daar kunnen ook psychologische aspecten een rol spelen; necebo effect? Daar ga ik komend semester mee aan de slag met studenten.
Mijn jongste lag in stuitligging. Daar kwamen ze pas in het ziekenhuis achter bij 9cm ontsluiting. Het was middernacht. Geen tijd om een keizersnee team op te roepen. Ik vroeg aan de gyneacoloog hoe vaak ze een stuitliggingsbevalling doen. Wat ik ook probeerde, ik kreeg geen kwantitatieve informatie. (Niet vaak, na aandringen niet elke maand). Er volgde een heel spannend uurtje. Bevalling goed en natuurlijk verlopen.
Persoonlijk heb ik veel liever dat een kans in een getal/percentage wordt uitgedrukt, dan kwalitatief omschreven met wat jullie een kanswoord noemen. Maar ik beschouw mezelf als hooggecijferd, niet de gemiddelde Nederlander dus. Ik zou ervoor willen pleiten dat kansen in het algemeen hybride worden weergegeven, daarmee bedoel ik: zowel met een kanswoord voor wie dat makkelijk (maar helaas vaak verkeerd) begrijpt, als kwantitatief, bijvoorbeeld als percentage.
Ik ook, en het allerliefst zie ik ook nog iets over de nauwkeurigheid van de schatting.
Het kan nog erger;: vaak wordt er gezegd : de kans is niet heel groot dat …
Dat kan heel klein tot en met groot betekenen
Jan karel zuur kno arts. bd