Moet je altijd bij het begin beginnen?

In haar laatste post schreef Winnifred Wijnker over drie soorten misleiding bij grafieken. Ze waarschuwde dat een verticale as die niet op nul begint misleidend kan zijn. Daar ben ik het zeker mee eens; als een grafiek niet op nul begint, dan moet je goed naar de as kijken. Maar, soms kan een grafiek juist misleidend zijn wanneer de y-as wél op nul begint. Het verschil zit hem in het type diagram. Geven punten, lijnen of staven de waarden aan?

Verschillende type diagrammen

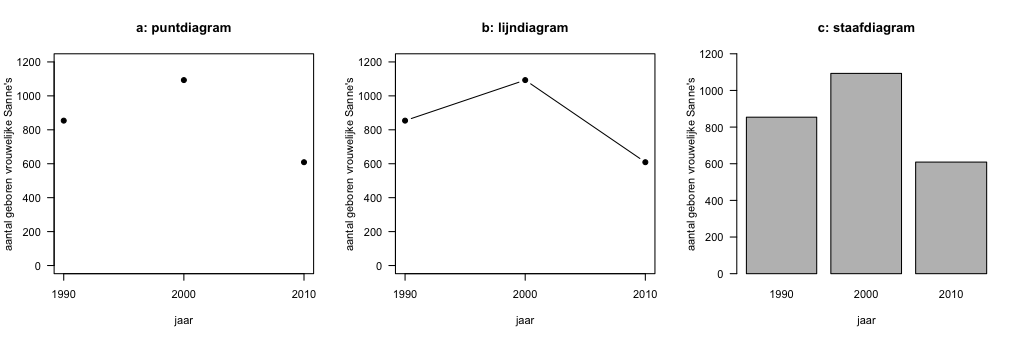
Laten we beginnen met de simpelste: het puntdiagram. Dit diagram geeft waarden in punten aan. Als voorbeeld geef ik in Figuur 1a met punten weer wat het aantal geboren meisjes die de naam “Sanne” kregen in de jaren 1990, 2000 en 2010 was. Vaak verbinden we deze punten nog met elkaar om een trend aan te geven en zo krijgen we een lijndiagram. Dit is vooral zinnig wanneer er de horizontale as een continue schaal heeft en de waarden op de lijn daardoor ook een interpretatie hebben. In het voorbeeld in Figuur 1b zou je de waarden op de lijnen kunnen interpreteren als een schatting van het aantal geboren Sanne’s in de maanden of dagen tussen 1990 en 2010.

Bij deze twee soorten grafieken geeft alleen de plaats van de punten of de hoogte van de lijn de waarden op de verticale as aan. Dat is anders bij staafdiagrammen.

Een staafdiagram bestaat uit staven waarvan de bovenkant van elke staaf de waarde op de verticale as aangeeft. Elke staaf representeert de waarde van bijvoorbeeld een groep of jaar. Zo geven de staven in Figuur 1c het aantal nieuwe Sanne’s in 1990, 2000 en 2010 weer.

Maar staven zijn twee dimensionale objecten en hebben daarom ook een lengte en oppervlakte. Dus eigenlijk geeft niet alleen het eindpunt van de staaf de waarden weer, maar óók de lengte en oppervlakte. En daarin zit het cruciale verschil met betrekking tot het wel of niet starten op de nullijn.

Staafdiagram: verticale as moet op nul beginnen

Mensen zijn erg visueel ingesteld en kijken vaak eerst naar vormen in plaats van naar tekst. Dus als jij naar een staafgrafiek kijkt, valt de lengte van de staven je waarschijnlijk het meeste op. Je eerste indruk van de verschillen tussen de staven komt dus door die lengte, niet door de waarden op de y-as.

Wanneer de verticale as niet op nul begint kort dit de staven in. Daardoor is de lengte van elke staaf geen juiste weergave meer van de echte waarde die hij representeert. Hierdoor lijken verschillen vaak groter dan ze echt zijn en dit vertroebelt jouw eerste indruk van het diagram.

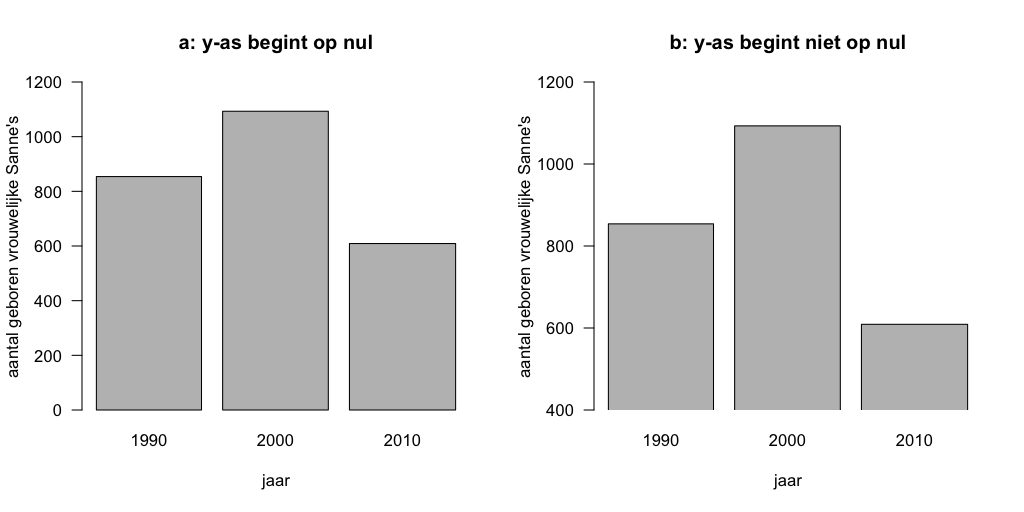
Kijk bijvoorbeeld naar twee staafdiagrammen in Figuur 2. In het linker diagram begint de verticale as wel op nul en in het rechter diagram niet. In principe zien we dezelfde data, maar we zien in eerste instantie rechts een veel groter verschil tussen de jaren 2000 en 2010 dan links. Alleen door goed te kijken naar de waarden op de verticale assen kun je achterhalen dat de verschillen eigenlijk gelijk zijn.

Om te zorgen dat de lengte van de staven representatief is voor de waarden die zij weergeven is de nullijn dus cruciaal. Een ingekorte staafdiagram geeft verschillen tussen staven misleidend weer.

Punt- of lijndiagram: verticale as moet logisch zijn

Waar bij staafdiagrammen de y-as altijd op nul moet beginnen, hoeft dat bij punt- of lijndiagrammen niet. Bij deze twee type diagrammen geven alleen de plaats van de punten of van de lijn de waarden van de grafiek weer. Of de verticale as nou wel of niet op nul begint, je moet dus altijd de waarden op die as bekijken om de grafiek af te lezen. Het is daarom minder van belang of de verticale as wel of niet op nul begint.

Bij dit type diagrammen is het daarom vooral belangrijk dat de verticale as logisch gekozen wordt, ofwel passend bij de data. Een typisch voorbeeld hiervoor is temperatuur.

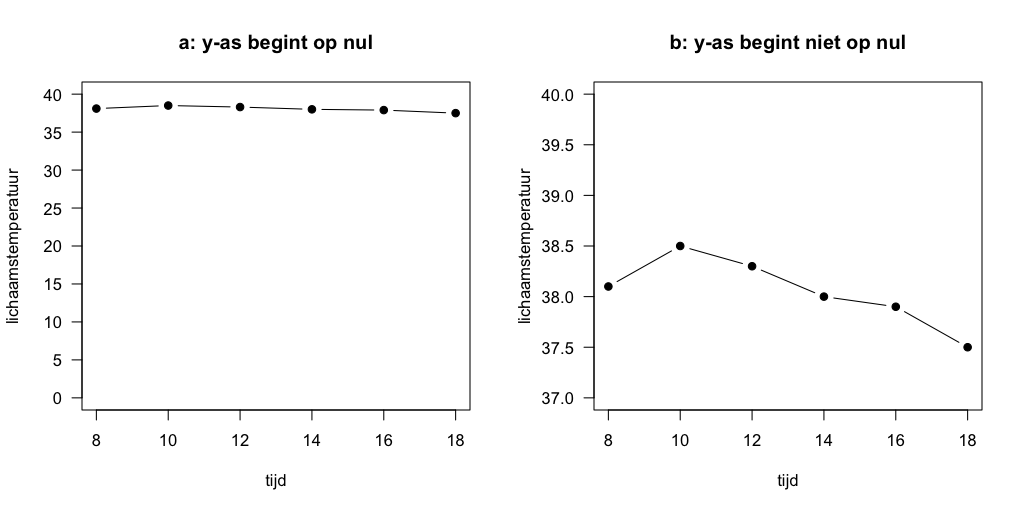
Stel bijvoorbeeld dat je ’s morgens wakker wordt met koorts. Als je gedurende de dag regelmatig je lichaamstemperatuur meet, kun je deze weergeven in een lijndiagram. Wanneer je dit diagram op nul laat beginnen, dan zie je waarschijnlijk een lijn die bijna vlak is, zoals in Figuur 3a. Dit komt doordat lichaamstemperatuur bij koorts waarschijnlijk tussen 37 en 40 graden blijft. Alle waarden onder de 37 graden zijn niet van belang, maar door deze toch weer te geven zijn de relevante temperatuurverschillen bijna niet meer zichtbaar.

In zo’n geval is het veel logischer om de nullijn weg te laten en een passendere as te kiezen, bijvoorbeeld een met de meest relevante temperaturen van 37 tot 40 graden, zoals in Figuur 3b. Omdat deze y-as inzoomt op waarden die van belang zijn, krijg je veel meer inzicht in de ontwikkeling van de koorts.

Bij een punt- en lijndiagram moet je er dus vooral op letten dat een verticale as de relevante waarden weergeeft. Als een as slecht gekozen is, door bijvoorbeeld op de nullijn te beginnen, verdoezelt dit de kleine verschillen. Dit is misleidend als juist kleine verschillen al relevant zijn.

Advies

Kijk bij het aflezen van een grafiek daarom altijd naar de combinatie van het type grafiek en de gekozen verticale as. Zo laat je je niet misleiden!

Bronnen / verder lezen:

Franconeri, S. L., Padilla, L. M., Shah, P., Zacks, J. M., & Hullman, J. (2021). The Science of Visual Data Communication: What Works. Psychological Science in the Public Interest, 22(3), 110–161. https://doi.org/10.1177/15291006211051956

Alberto Cairo (2020) How Charts Lie – Getting Smarter about Visual Information. Ww Norton & Co.

Hoofdfoto: colorful pencils,Sadhana@1986 op Pixahive